题目内容
11.如图是某算法的流程图,若输出的y值是2,则输入的x的值是-1或4.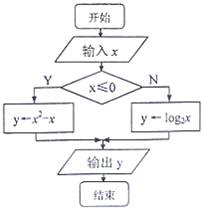
分析 解:模拟执行程序框图,可得程序框图的功能是求y=$\left\{\begin{array}{l}{{x}^{2}-x}&{x≤0}\\{{log}_{2}x}&{x>0}\end{array}\right.$的值,y=2,分情况讨论即可求得x的值.
解答 解:模拟执行程序框图,可得程序框图的功能是求y=$\left\{\begin{array}{l}{{x}^{2}-x}&{x≤0}\\{{log}_{2}x}&{x>0}\end{array}\right.$的值,
∵y=2,
∴当x≤0时,x2-x=2,解得:x=-1或2(舍去);
当x>0时,log2x=2,解得:x=4;
综上,输入的x的值是:-1或4.
故答案为:-1或4.
点评 本题主要考查解程序框图和算法,属于基本知识的考查.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
2.若{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}是空间的一个基底,则下列各组中不能构成空间一个基底的是( )
| A. | $\overrightarrow{a}$,2$\overrightarrow{b}$,3$\overrightarrow{c}$ | B. | $\overrightarrow{a}$+$\overrightarrow{b}$,$\overrightarrow{b}$$+\overrightarrow{c}$,$\overrightarrow{c}$$+\overrightarrow{a}$ | C. | $\overrightarrow{a}$+2$\overrightarrow{b}$,2$\overrightarrow{b}$+3$\overrightarrow{c}$,3$\overrightarrow{a}$-9$\overrightarrow{c}$ | D. | $\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$,$\overrightarrow{b}$,$\overrightarrow{c}$ |
19.在锐角△ABC中,$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{CA}$=$\overrightarrow{b}$,S△ABC=1,且|$\overrightarrow{a}$|=2,|$\overrightarrow{b}$|=$\sqrt{2}$,则$\overrightarrow{a}$•$\overrightarrow{b}$等于( )
| A. | -2 | B. | 2 | C. | -$\frac{1}{2}$ | D. | $\frac{1}{2}$ |
1.定义在R上的奇函数f(x)满足f(x+1)=f(-x),当x∈(0,$\frac{1}{2}$)时,f(x)=log${\;}_{\frac{1}{2}}$(1-x),则f(x)在区间(1,$\frac{3}{2}$)内是( )
| A. | 是减函数,且f(x)>0 | B. | 是减函数,且f(x)<0 | C. | 是增函数,且f(x)>0 | D. | 是增函数,且f(x)<0 |