题目内容
17.已知函数f(x)=2sin(ωx+$\frac{π}{3}$)(ω>0)的图象上两个相邻的最高点间的距离是π.(1)求函数f(x)的表达式,并在平面直角坐标系中用“五点法”作出该函数的一个周期内的图象;
(2)当x∈[0,$\frac{π}{4}$]时,求函数f(x)的值域.
分析 (1)利用正弦函数的周期性求出ω,可得函数的解析式,再利用五点法作y=Asin(ωx+φ)在一个周期上的简图.
(2)由条件利用正弦函数的定义域和值域,求得函数f(x)的值域.
解答 解:(1)∵函数f(x)=2sin(ωx+$\frac{π}{3}$)(ω>0)的图象上两个相邻的最高点间的距离是$\frac{2π}{ω}$=π,
∴ω=2,f(x)=2sin(2x+$\frac{π}{3}$).
列表:
| 2x+$\frac{π}{3}$ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | -$\frac{π}{6}$ | $\frac{π}{12}$ | $\frac{π}{3}$ | $\frac{7π}{12}$ | $\frac{5π}{6}$ |
| f(x) | 0 | 2 | 0 | -2 | 0 |
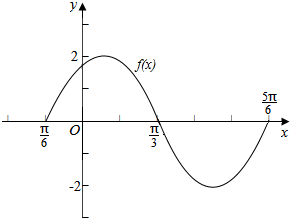
(2)当x∈[0,$\frac{π}{4}$]时,2x+$\frac{π}{3}$∈[$\frac{π}{3}$,$\frac{5π}{6}$],sin(2x+$\frac{π}{3}$)∈[$\frac{1}{2}$,1],函数f(x)=2sin(2x+$\frac{π}{3}$)∈[1,2],
即函数f(x)的值域为[1,2].
点评 本题主要考查函数y=Asin(ωx+φ)的周期性,用五点法作y=Asin(ωx+φ)在一个周期上的简图,正弦函数的定义域和值域,属于基础题.

练习册系列答案
相关题目
2.若{$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$}是空间的一个基底,则下列各组中不能构成空间一个基底的是( )
| A. | $\overrightarrow{a}$,2$\overrightarrow{b}$,3$\overrightarrow{c}$ | B. | $\overrightarrow{a}$+$\overrightarrow{b}$,$\overrightarrow{b}$$+\overrightarrow{c}$,$\overrightarrow{c}$$+\overrightarrow{a}$ | C. | $\overrightarrow{a}$+2$\overrightarrow{b}$,2$\overrightarrow{b}$+3$\overrightarrow{c}$,3$\overrightarrow{a}$-9$\overrightarrow{c}$ | D. | $\overrightarrow{a}$+$\overrightarrow{b}$+$\overrightarrow{c}$,$\overrightarrow{b}$,$\overrightarrow{c}$ |