题目内容
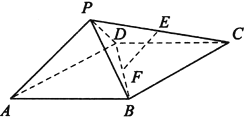
【题目】如图,四棱锥P—ABCD中,ABCD为矩形,△PAD为等腰直角三角形,
∠APD=90°,面PAD⊥面ABCD,且AB=1,AD=2,E、F分别为PC和BD的中点.
(1)证明:EF∥面PAD;
(2)证明:面PDC⊥面PAD;
(3)求四棱锥P—ABCD的体积.
【答案】(1)见解析(2)见解析(3)![]()
【解析】试题分析: (1)确定出EF∥AP,运用判断定理可证明.(2)抓住CD⊥AD,CD⊥面PAD,运用面面垂直的定理可证明.(3)确定PO为四棱锥P﹣ABCD的高.
求出PO=1,运用体积公式V=![]() PO×AB×AD求解即可.
PO×AB×AD求解即可.
试题解析:
(1)如图,连接AC,∵ABCD为矩形且F是BD的中点,∴AC必经过F,又E是PC的中点,所以,EF∥AP
∵EF在面PAD外,PA在面内,∴EF∥面PAD

(2)∵面PAD⊥面ABCD,CD⊥AD,面PAD![]() 面ABCD=AD,∴CD⊥面PAD,又AP
面ABCD=AD,∴CD⊥面PAD,又AP![]() 面PAD,∴AP⊥CD又∵AP⊥PD,PD和CD是相交直线且在面PDC内,∴AP⊥面PCD,又AD
面PAD,∴AP⊥CD又∵AP⊥PD,PD和CD是相交直线且在面PDC内,∴AP⊥面PCD,又AD![]() 面PAD,所以,面PDC⊥面PAD
面PAD,所以,面PDC⊥面PAD
(3)取AD中点为O,连接PO,因为面PAD⊥面ABCD及△PAD为等腰直角三角形,所以PO⊥面ABCD,即PO为四棱锥P—ABCD的高,∵AD=2,∴PO=1,
所以四棱锥P—ABCD的体积![]()

【题目】已知产品![]() 的质量采用综合指标值
的质量采用综合指标值![]() 进行衡量,
进行衡量,![]() 为一等品;
为一等品;![]() 为二等品;
为二等品;![]() 为三等品.我市一家工厂准备购进新型设备以提高生产产品
为三等品.我市一家工厂准备购进新型设备以提高生产产品![]() 的效益,在某供应商提供的设备中任选一个试用,生产了一批产品并统计相关数据,得到频率分布直方图:
的效益,在某供应商提供的设备中任选一个试用,生产了一批产品并统计相关数据,得到频率分布直方图:
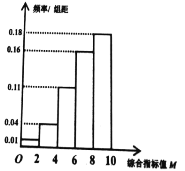
(1)估计该新型设备生产的产品![]() 为二等品的概率;
为二等品的概率;
(2)根据这家工厂的记录,产品各等次的销售率(某等次产品销量与其对应产量的比值)及单件售价情况如下:
一等品 | 二等品 | 三等品 | |
销售率 |
|
|
|
单件售价 |
|
|
|
根据以往的销售方案,未售出的产品统一按原售价的![]() 全部处理完.已知该工厂认购该新型设备的前提条件是,该新型设备生产的产品同时满足下列两个条件:
全部处理完.已知该工厂认购该新型设备的前提条件是,该新型设备生产的产品同时满足下列两个条件:
①综合指标值的平均数不小于![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
②单件平均利润值不低于![]() .
.
若该新型设备生产的产品![]() 的成本为
的成本为![]() 元/件,月产量为
元/件,月产量为![]() 件,在销售方案不变的情况下,根据以上图表数据,分析该新型设备是否达到该工厂的认购条件.
件,在销售方案不变的情况下,根据以上图表数据,分析该新型设备是否达到该工厂的认购条件.