��Ŀ����
����Ŀ����֪��Ʒ![]() �����������ۺ�ָ��ֵ
�����������ۺ�ָ��ֵ![]() ���к�����
���к�����![]() Ϊһ��Ʒ��
Ϊһ��Ʒ��![]() Ϊ����Ʒ��
Ϊ����Ʒ��![]() Ϊ����Ʒ.����һ�ҹ��������������豸�����������Ʒ
Ϊ����Ʒ.����һ�ҹ��������������豸�����������Ʒ![]() ��Ч�棬��ij��Ӧ���ṩ���豸����ѡһ�����ã�������һ����Ʒ��ͳ��������ݣ��õ�Ƶ�ʷֲ�ֱ��ͼ��
��Ч�棬��ij��Ӧ���ṩ���豸����ѡһ�����ã�������һ����Ʒ��ͳ��������ݣ��õ�Ƶ�ʷֲ�ֱ��ͼ��
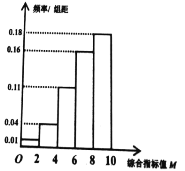
��1�����Ƹ������豸�����IJ�Ʒ![]() Ϊ����Ʒ�ĸ��ʣ�
Ϊ����Ʒ�ĸ��ʣ�
��2��������ҹ����ļ�¼����Ʒ���ȴε������ʣ�ij�ȴβ�Ʒ���������Ӧ�����ı�ֵ���������ۼ�������£�
һ��Ʒ | ����Ʒ | ����Ʒ | |
������ |
|
|
|
�����ۼ� |
|
|
|
�������������۷�����δ�۳��IJ�Ʒͳһ��ԭ�ۼ۵�![]() ȫ��������.��֪�ù����Ϲ��������豸��ǰ�������ǣ��������豸�����IJ�Ʒͬʱ������������������
ȫ��������.��֪�ù����Ϲ��������豸��ǰ�������ǣ��������豸�����IJ�Ʒͬʱ������������������
���ۺ�ָ��ֵ��ƽ������С��![]() ��ͬһ���е������ø���������е�ֵ����������
��ͬһ���е������ø���������е�ֵ����������
�ڵ���ƽ������ֵ������![]() .
.
���������豸�����IJ�Ʒ![]() �ijɱ�Ϊ
�ijɱ�Ϊ![]() Ԫ/�����²���Ϊ
Ԫ/�����²���Ϊ![]() ���������۷������������£���������ͼ�����ݣ������������豸�Ƿ�ﵽ�ù������Ϲ�����.
���������۷������������£���������ͼ�����ݣ������������豸�Ƿ�ﵽ�ù������Ϲ�����.
���𰸡�(1) �¼�![]() �ĸ��ʹ���ֵΪ
�ĸ��ʹ���ֵΪ![]() ;(2)������.
;(2)������.
����������������1������Ƶ�ʷֲ�ֱ��ͼ�е�Ƶ�ʼ��㼴������2������Ƶ�ʷֲ�ֱ��ͼ����ۺ�ָ��ֵ��ƽ������Ȼ���ٸ��������������ƽ������ֵ��������������жϿɵý��ۣ�
��⣺��1����![]() Ϊ�¼����������豸�����IJ�Ʒ
Ϊ�¼����������豸�����IJ�Ʒ![]() Ϊ����Ʒ��.
Ϊ����Ʒ��.
��ֱ��ͼ��֪���������豸�����IJ�Ʒ![]() Ϊ����Ʒ��Ƶ��Ϊ��
Ϊ����Ʒ��Ƶ��Ϊ��
![]() ��
��
���¼�![]() �ĸ��ʹ���ֵΪ
�ĸ��ʹ���ֵΪ![]() .
.
��2�����ȷ����������豸�����IJ�Ʒ![]() ���ۺ�ָ��ֵ��ƽ������
���ۺ�ָ��ֵ��ƽ������
��ֱ��ͼ��֪�ۺ�ָ��ֵ��ƽ����
![]()
![]() .
.
���Ը��豸�������IJ�Ʒ![]() ���ۺ�ָ��ֵ��ƽ�����Ĺ���ֵ
���ۺ�ָ��ֵ��ƽ�����Ĺ���ֵ![]() ��
��
�������Ϲ�������.
���ٷ�����Ҥ¯���Ƶĵ���ƽ������ֵ��
��ֱ��ͼ��֪���豸�������IJ�Ʒ![]() Ϊһ����������Ʒ�ĸ��ʹ���ֵ�ֱ�Ϊ��
Ϊһ����������Ʒ�ĸ��ʹ���ֵ�ֱ�Ϊ��![]() ��
��![]() ��
��![]() .
.
��![]() ����Ʒ�У�һ����������Ʒ�ļ�������ֵ�ֱ�Ϊ��
����Ʒ�У�һ����������Ʒ�ļ�������ֵ�ֱ�Ϊ��![]() ����
����![]() ����
����![]() ��.
��.
һ��Ʒ������������Ϊ![]() Ԫ��
Ԫ��
����Ʒ������������Ϊ![]() Ԫ��
Ԫ��
����Ʒ������������Ϊ![]() Ԫ.
Ԫ.
��![]() ����Ʒ�ĵ���ƽ������ֵ�Ĺ���ֵΪ��
����Ʒ�ĵ���ƽ������ֵ�Ĺ���ֵΪ��
![]() Ԫ.
Ԫ.
�����Ϲ�������.
�����������������豸�ﵽ�Ϲ�����.

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ��ij��˾Ϊȷ����һ���Ͷ��ij�ֲ�Ʒ�������ѣ����˽���������![]() ����λ����Ԫ������������
����λ����Ԫ������������![]() ����λ���֣���Ӱ�죬�Խ��������������
����λ���֣���Ӱ�죬�Խ��������������![]() ����������
����������![]() (
(![]() )���������˳���ͳ�ƣ��õ��������ݣ�
)���������˳���ͳ�ƣ��õ��������ݣ�
��ݣ� | 2012 | 2013 | 2014 | 2015 | 2016 | 2017 |
�������� | 23 | 25 | 27 | 29 | 32 | 35 |
�������� | 11 | 21 | 24 | 66 | 115 | 325 |
��1������ɢ��ͼ�ж�![]() ��
��![]() ����һ�����ʺ���Ϊ��������
����һ�����ʺ���Ϊ��������![]() ���֣������������
���֣������������![]() ����Ԫ���Ļع鷽�����ͣ�
����Ԫ���Ļع鷽�����ͣ�
��2���涨����Ʒ����������![]() ���֣�����������
���֣�����������![]() ����Ԫ���ı�ֵ����1ʱ����Ϊ����Ч�����ã��ִ���6������ѡ3�꣬������ѡ��Ч�����õ�����Ϊ
����Ԫ���ı�ֵ����1ʱ����Ϊ����Ч�����ã��ִ���6������ѡ3�꣬������ѡ��Ч�����õ�����Ϊ![]() ������
������![]() ������ȡֵ�������Ӧ�ĸ��ʣ�
������ȡֵ�������Ӧ�ĸ��ʣ�
��3������Ƶ�ʷֲ�ֱ��ͼ�������������ƽ������˼�뷽������![]() ��ƽ����.
��ƽ����.