题目内容
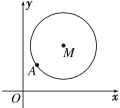
【题目】如图，在平面直角坐标系xOy中，已知以M为圆心的圆M：x2＋y2－12x－14y＋60＝0及其上一点A(2，4）．
（1）设圆N与x轴相切，与圆M外切，且圆心N在直线x＝6上，求圆N的标准方程；
（2）设平行于OA的直线l与圆M相交于B，C两点，且BC＝OA，
求直线l的方程．
【答案】（1）
；（2）
【解析】
分析：(1)化简得到圆
的标准方程，求得圆的圆心坐标和半径，进而求得N的标准方程；
(2)由题意得
，设
，则圆心到直线
的距离，由此能求出直线的方程.
详解：圆M的标准方程为(x－6)2＋(y－7)2＝25，
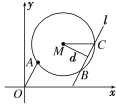
所以圆心M(6,7)，半径为5.
(1)圆N的标准方程为(x－6)2＋(y－1)2＝1.
(2)因为直线l∥OA，所以直线l的斜率为
＝2
设直线l的方程为y＝2x＋m，即2x－y＋m＝0，
因为BC＝OA＝＝2，而MC2＝d2＋
2，
则圆心M到直线l的距离d＝＝
所以解得m＝5或m＝－15.
故直线l的方程为2x－y＋5＝0或2x－y－15＝0
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
【题目】某商场经销一批进价为每件30元的商品，在市场试销中发现，此商品的销售单价x(元)与日销售量y(件)之间有如下表所示的关系：
x | 30 | 40 | 45 | 50 |
y | 60 | 30 | 15 | 0 |
在所给的坐标图纸中，根据表中提供的数据，描出实数对(x，y)的对应点，并确定y与x的一个函数关系式；
(2)设经营此商品的日销售利润为P元，根据上述关系，写出P关于x的函数关系式，并指出销售单价x为多少元时，才能获得最大日销售利润？
