题目内容
9.椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的右焦点F(c,0)关于直线y=$\frac{b}{c}$x的对称点Q在椭圆上,则椭圆的离心率是$\frac{\sqrt{2}}{2}$.分析 设出Q的坐标,利用对称知识,集合椭圆方程推出椭圆几何量之间的关系,然后求解离心率即可.
解答 解:设Q(m,n),由题意可得$\left\{\begin{array}{l}\frac{n}{m-c}=-\frac{c}{b}…①\\ \frac{n}{2}=\frac{b}{c}•\frac{m+c}{2}…②\\ \frac{{m}^{2}}{{a}^{2}}+\frac{{n}^{2}}{{b}^{2}}=1…③\end{array}\right.$,
由①②可得:m=$\frac{{c}^{3}-{cb}^{2}}{{a}^{2}}$,n=$\frac{2{bc}^{2}}{{a}^{2}}$,代入③可得:$\frac{{(\frac{{c}^{3}-{cb}^{2}}{{a}^{2}})}^{2}}{{a}^{2}}+\frac{{(\frac{2{bc}^{2}}{{a}^{2}})}^{2}}{{b}^{2}}=1$,
可得,4e6+e2-1=0.
即4e6-2e4+2e4-e2+2e2-1=0,
可得(2e2-1)(2e4+e2+1)=0
解得e=$\frac{\sqrt{2}}{2}$.
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题考查椭圆的方程简单性质的应用,考查对称知识以及计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
18.设f(x)是定义在R上的偶函数,且当x≥0时,f(x)=$\left\{\begin{array}{l}{{x}^{2}-1,0≤x<1}\\{lnx,x≥1}\end{array}\right.$,若对任意的x∈[a,a+1],不等式f(2x)≤f(x+a)恒成立,则实数a的最大值为( )
| A. | -1 | B. | -$\frac{2}{3}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{3}{4}$ |
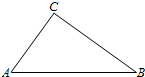 如图,A,B,C三地有直道相通,AB=5千米,AC=3千米,BC=4千米.现甲、乙两警员同时从A地出发匀速前往B地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是AB,速度为5千米/小时,乙的路线是ACB,速度为8千米/小时.乙到达B地后原地等待.设t=t1时乙到达C地.
如图,A,B,C三地有直道相通,AB=5千米,AC=3千米,BC=4千米.现甲、乙两警员同时从A地出发匀速前往B地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是AB,速度为5千米/小时,乙的路线是ACB,速度为8千米/小时.乙到达B地后原地等待.设t=t1时乙到达C地. ,
,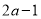 ,
,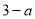 .则这个数列的通项公式为_______.
.则这个数列的通项公式为_______. .
. 对其定义域内任意
对其定义域内任意 成立,求
成立,求 值;
值; 时,求
时,求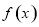 在区间
在区间 上的最值.
上的最值.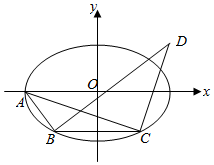 如图,在平面直角坐标系xOy中,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左顶点为A,与x轴平行的直线与椭圆E交于B、C两点,过B、C两点且分别与直线AB、AC垂直的直线相交于点D.已知椭圆E的离心率为$\frac{{\sqrt{5}}}{3}$,右焦点到右准线的距离为$\frac{{4\sqrt{5}}}{5}$.
如图,在平面直角坐标系xOy中,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左顶点为A,与x轴平行的直线与椭圆E交于B、C两点,过B、C两点且分别与直线AB、AC垂直的直线相交于点D.已知椭圆E的离心率为$\frac{{\sqrt{5}}}{3}$,右焦点到右准线的距离为$\frac{{4\sqrt{5}}}{5}$.