题目内容
11.设集合A={x|x2-4x+3=0}与B={x|ax-3=0},且B⊆A求实数a构成的集合.分析 先化简集合A,B,在根据B⊆A即可求出a的值,问题得以解决.
解答 解:A={x|x2-4x+3=0}={1,3},
当a=0时,B=∅,
当a≠0时,B={$\frac{3}{a}$},
∵B⊆A,
∴B=∅,或B={1}或B={3},
∴a=0,或$\frac{3}{a}$=1,或$\frac{3}{a}$=3,
即a=0,或a=3,或a=9,
∴实数a构成的集合为{0,3,9}
点评 本题考查了集合的包含关系,以及集合的表示方法,属于基础题.

练习册系列答案
相关题目
18.设f(x)是定义在R上的偶函数,且当x≥0时,f(x)=$\left\{\begin{array}{l}{{x}^{2}-1,0≤x<1}\\{lnx,x≥1}\end{array}\right.$,若对任意的x∈[a,a+1],不等式f(2x)≤f(x+a)恒成立,则实数a的最大值为( )
| A. | -1 | B. | -$\frac{2}{3}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{3}{4}$ |
 .
. 对其定义域内任意
对其定义域内任意 成立,求
成立,求 值;
值; 时,求
时,求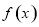 在区间
在区间 上的最值.
上的最值.