题目内容
6.在△ABC中,已知AB=$\frac{4\sqrt{6}}{3}$,cosB=$\frac{\sqrt{6}}{6}$,AC边上的中线BD=$\sqrt{5}$,求边长BC的值.分析 延长BD至E,使得DE=BD,连接CE,△BCE中,由余弦定理建立方程,即可求边长BC的值.
解答 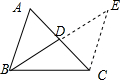 解:延长BD至E,使得DE=BD,连接CE,则cos∠BCE=-$\frac{\sqrt{6}}{6}$,CE=$\frac{4\sqrt{6}}{3}$,BE=2$\sqrt{5}$,
解:延长BD至E,使得DE=BD,连接CE,则cos∠BCE=-$\frac{\sqrt{6}}{6}$,CE=$\frac{4\sqrt{6}}{3}$,BE=2$\sqrt{5}$,
△BCE中,由余弦定理可得20=($\frac{4\sqrt{6}}{3}$)2+BC2-2×$\frac{4\sqrt{6}}{3}$×BC×(-$\frac{\sqrt{6}}{6}$),
∴BC2+$\frac{8}{3}$BC-$\frac{28}{3}$=0,
∴BC=2(负数舍去).
点评 本题考查余弦定理,考查学生的计算能力,比较基础.

练习册系列答案
相关题目
18.设f(x)是定义在R上的偶函数,且当x≥0时,f(x)=$\left\{\begin{array}{l}{{x}^{2}-1,0≤x<1}\\{lnx,x≥1}\end{array}\right.$,若对任意的x∈[a,a+1],不等式f(2x)≤f(x+a)恒成立,则实数a的最大值为( )
| A. | -1 | B. | -$\frac{2}{3}$ | C. | -$\frac{1}{2}$ | D. | -$\frac{3}{4}$ |
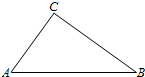 如图,A,B,C三地有直道相通,AB=5千米,AC=3千米,BC=4千米.现甲、乙两警员同时从A地出发匀速前往B地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是AB,速度为5千米/小时,乙的路线是ACB,速度为8千米/小时.乙到达B地后原地等待.设t=t1时乙到达C地.
如图,A,B,C三地有直道相通,AB=5千米,AC=3千米,BC=4千米.现甲、乙两警员同时从A地出发匀速前往B地,经过t小时,他们之间的距离为f(t)(单位:千米).甲的路线是AB,速度为5千米/小时,乙的路线是ACB,速度为8千米/小时.乙到达B地后原地等待.设t=t1时乙到达C地.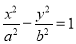 (
(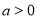 ,
,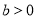 )经过点
)经过点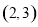 ,且离心率为
,且离心率为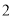 ,则它的焦距为( )
,则它的焦距为( )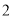 B.
B.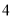
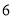 D.
D.