题目内容
若a,b为非零向量且a∥b,
1,2∈R,且12≠0.
求证：1a+2b与1a-2b为共线向量.
1,2∈R,且12≠0.求证：
1a+2b与1a-2b为共线向量.证明见解析
证明 设a=(x1,y1),b=(x2,y2).
∵a∥b,b≠0,a≠0,∴存在实数m,使得a=mb,
即a=(x1,y1)=(mx2,my2),
∴1a+2b=((m1+2)x2,(m1+2)y2)
=(m1+2)(x2,y2)
同理1a-2b=(m1-2)(x2,y2),
∴(1a+2b)∥(1a-2b)∥b,
而b≠0,∴(1a+2b)∥(1a-2b).
∵a∥b,b≠0,a≠0,∴存在实数m,使得a=mb,
即a=(x1,y1)=(mx2,my2),
∴
1a+2b=((m1+2)x2,(m1+2)y2)=(m
1+2)(x2,y2)同理
1a-2b=(m1-2)(x2,y2),∴(
1a+2b)∥(1a-2b)∥b,而b≠0,∴(
1a+2b)∥(1a-2b).
练习册系列答案
相关题目
=
，
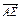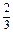
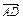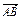=a，
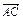=b.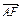
、
、
；
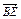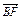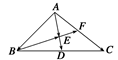
，则以下说法错误的是（ ）
相等的向量只有一个（不含
的模恰为
模的
倍
与
与
共线，
共线，则
，则
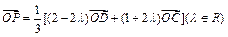，则点P的轨迹一定过△ABC （ ）
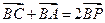，则（ ）
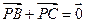
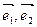是不共线的向量,已知向量
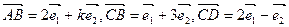,若A,B,D三点共线,求k的值
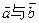夹角为60°，