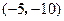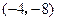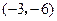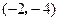题目内容
如图所示,在△ABC中,D、F分别是BC、AC的中点,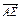 =
=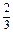
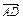 ,
,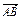 =a,
=a,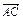 =b.
=b.
(1)用a、b表示向量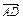 、
、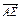 、
、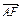 、
、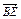 、
、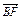 ;
;
(2)求证:B、E、F三点共线.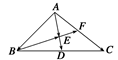
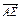 =
=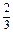
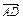 ,
,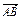 =a,
=a,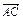 =b.
=b.(1)用a、b表示向量
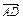 、
、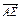 、
、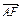 、
、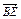 、
、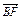 ;
;(2)求证:B、E、F三点共线.

(1)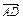 =
=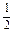 (a+b),
(a+b), 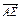 =
=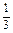 (a+b).
(a+b).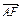 =
=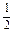 b,
b,

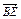 =
=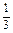 (b-2a).
(b-2a).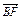 =
=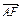 -
-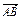 =
=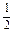 (b-2a).
(b-2a).
(2)证明见解析
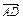 =
=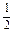 (a+b),
(a+b), 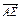 =
=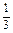 (a+b).
(a+b).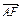 =
=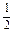 b,
b,
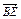 =
=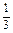 (b-2a).
(b-2a).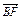 =
=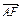 -
-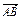 =
=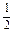 (b-2a).
(b-2a).(2)证明见解析
(1)解 延长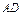 到G,使
到G,使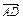 =
=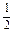
 ,
,
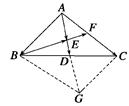
连接BG、CG,得到平行四边形ABGC,
所以 =a+b,
=a+b,
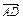 =
=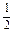
 =
=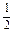 (a+b),
(a+b),
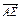 =
=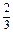
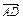 =
=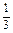 (a+b).
(a+b).
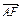 =
=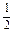
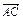 =
=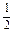 b,
b,
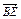 =
=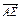 -
-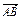 =
=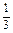 (a+b)-a=
(a+b)-a=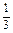 (b-2a).
(b-2a).
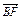 =
=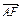 -
-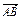 =
=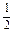 b-a=
b-a=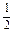 (b-2a).
(b-2a).
(2)证明 由(1)可知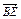 =
=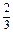
 ,所以B、E、F三点共线.
,所以B、E、F三点共线.
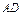 到G,使
到G,使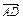 =
=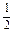
 ,
,
连接BG、CG,得到平行四边形ABGC,
所以
 =a+b,
=a+b,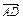 =
=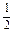
 =
=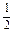 (a+b),
(a+b), 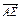 =
=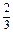
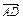 =
=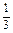 (a+b).
(a+b).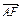 =
=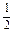
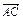 =
=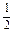 b,
b,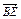 =
=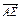 -
-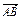 =
=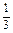 (a+b)-a=
(a+b)-a=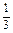 (b-2a).
(b-2a).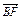 =
=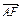 -
-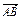 =
=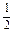 b-a=
b-a=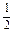 (b-2a).
(b-2a).(2)证明 由(1)可知
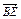 =
=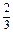
 ,所以B、E、F三点共线.
,所以B、E、F三点共线.
练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
 1,
1,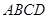 ,A
,A 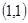 , B
, B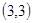 , C
, C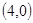 ,则 D 点坐标 ;
,则 D 点坐标 ;
 ,
, ,
, ,则向量
,则向量 在向量
在向量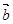 方向上的投影是( )
方向上的投影是( )



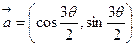 ,
,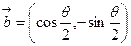 ,且
,且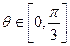 .
.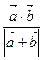 的最值;
的最值;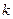 的值,使
的值,使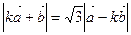
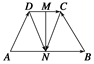
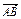 =a,
=a,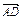 =b,
=b,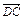 =c,试用a、b、c表示
=c,试用a、b、c表示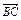 ,
,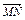 ,
,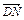 +
+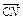 .
.
 、
、 是两个不共线的向量,若它们起点相同,
是两个不共线的向量,若它们起点相同, 、
、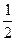
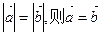
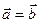 ,
,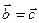 ,则
,则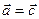 ;
;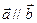 ,
,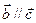 ,则
,则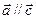 (8)若四边形ABCD是平行四边形,则
(8)若四边形ABCD是平行四边形,则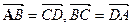
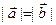 且
且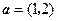 ,
,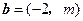 ,且
,且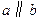 ,则
,则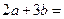 ( )
( )