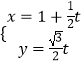题目内容
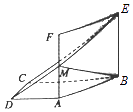
【题目】如图,点F是抛物线τ:x2=2py (p>0)的焦点,点A是抛物线上的定点,且 ![]() =(2,0),点B,C是抛物线上的动点,直线AB,AC斜率分别为k1 , k2 .
=(2,0),点B,C是抛物线上的动点,直线AB,AC斜率分别为k1 , k2 . 
( I)求抛物线τ的方程;
(Ⅱ)若k1﹣k2=2,点D是点B,C处切线的交点,记△BCD的面积为S,证明S为定值.
【答案】解:(Ⅰ)设A(x0,y0),可知F(0, ![]() ),故
),故 ![]() .
.
∴ 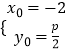 ,代入x2=2py,得p=2.
,代入x2=2py,得p=2.
∴抛物线τ的方程为x2=4y.
(Ⅱ)过D作y轴的平行线交BC于点E,并设B( ![]() ),C(
),C( ![]() ),
),
由(Ⅰ)得A(﹣2,1).
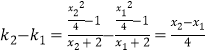 =2,
=2,
∴x2﹣x1=8.
直线DBy= ![]() ,直线CDy=
,直线CDy= ![]() ,解得
,解得  .
.
∴直线BC的方程为y﹣ ![]() =
= ![]() ,将xD代入得
,将xD代入得 ![]() .
.
∴△BCD的面积为S= ![]() ×ED×(x2﹣x1)=
×ED×(x2﹣x1)= ![]() =
= ![]() (定值)
(定值)
【解析】(Ⅰ)设A(x0,y0),可知F(0, ![]() ),故
),故 ![]() .求得A坐标,代入x2=2py,得p=2.即可(Ⅱ)过D作y轴的平行线交BC于点E,.并设B(
.求得A坐标,代入x2=2py,得p=2.即可(Ⅱ)过D作y轴的平行线交BC于点E,.并设B( ![]() ),C(
),C( ![]() ),由
),由 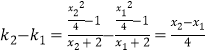 =2,得x2﹣x1=8.联立直线、直线方程得
=2,得x2﹣x1=8.联立直线、直线方程得  .由题意
.由题意 ![]() ,即可求△BCD的面积为S=
,即可求△BCD的面积为S= ![]() ×ED×(x2﹣x1)=
×ED×(x2﹣x1)= ![]() =
= ![]() (定值)
(定值)

 阅读快车系列答案
阅读快车系列答案【题目】中石化集团获得了某地深海油田区块的开采权,集团在该地区随机初步勘探了部分儿口井,取得了地质资料.进入全面勘探时期后,集团按网络点来布置井位进行全面勘探.由于勘探一口井的费用很高,如果新设计的井位与原有井位重合或接近,便利用旧井的地质资料,不必打这口新井,以节约勘探费用.勘探初期数据资料见如表:
井号I | 1 | 2 | 3 | 4 | 5 | 6 |
坐标(x,y)(km) | (2,30) | (4,40) | (5,60) | (6,50) | (8,70) | (1,y) |
钻探深度(km) | 2 | 4 | 5 | 6 | 8 | 10 |
出油量(L) | 40 | 70 | 110 | 90 | 160 | 205 |
(1)1~6号旧井位置线性分布,借助前5组数据求得回归直线方程为y=6.5x+a,求a,并估计y的预报值;
(2)现准备勘探新井7(1,25),若通过1、3、5、7号井计算出的 ![]() 的值(
的值( ![]() 精确到0.01)相比于(1)中b,a的值之差不超过10%,则使用位置最接近的已有旧井6(1,y),否则在新位置打开,请判断可否使用旧井? (参考公式和计算结果:
精确到0.01)相比于(1)中b,a的值之差不超过10%,则使用位置最接近的已有旧井6(1,y),否则在新位置打开,请判断可否使用旧井? (参考公式和计算结果: 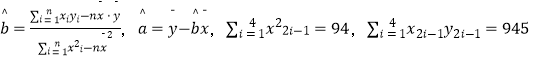 )
)
(3)设出油量与勘探深度的比值k不低于20的勘探并称为优质井,那么在原有井号1~6的出油量不低于50L的井中任意勘探3口井,求恰好2口是优质井的概率.
【题目】某汽车的使用年数x与所支出的维修费用y的统计数据如表:
使用年数x(单位:年) | 1 | 2 | 3 | 4 | 5 |
维修总费用y(单位:万元) | 0.5 | 1.2 | 2.2 | 3.3 | 4.5 |
根据上表可得y关于x的线性回归方程 ![]() =
= ![]() x﹣0.69,若该汽车维修总费用超过10万元就不再维修,直接报废,据此模型预测该汽车最多可使用( )
x﹣0.69,若该汽车维修总费用超过10万元就不再维修,直接报废,据此模型预测该汽车最多可使用( )
A.8年
B.9年
C.10年
D.11年