题目内容
【题目】某市为了鼓励市民节约用电,实行“阶梯式”电价,将该市每户居民的月用电量划分为三档,月用电量不超过200度的部分按0.5元/度收费,超过200度但不超过400度的部分按0.8元/度收费,超过400度的部分按1.0元/度收费.
(1)求某户居民用电费用 ![]() (单位:元)关于月用电量
(单位:元)关于月用电量 ![]() (单位:度)的函数解析式;
(单位:度)的函数解析式;
(2)为了了解居民的用电情况,通过抽样,获得了今年1月份100户居民每户的用电量,统计分析后得到如图所示的频率分布直方图,若这100户居民中,今年1月份用电费用不超过260元的点80%,求 ![]() 的值;
的值;
(3)在满足(2)的条件下,若以这100户居民用电量的频率代替该月全市居民用户用电量的概率,且同组中的数据用该组区间的中点值代替,记 ![]() 为该居民用户1月份的用电费用,求
为该居民用户1月份的用电费用,求 ![]() 的分布列和数学期望.
的分布列和数学期望.
【答案】
(1)
当 ![]() 时,
时, ![]() ;
;
当 ![]() 时,
时, ![]() ,
,
当 ![]() 时,
时, ![]() ,
,
所以 ![]() 与
与 ![]() 之间的函数解析式为:
之间的函数解析式为: 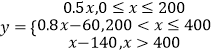 ;
;
(2)
由(1)可知:当 ![]() 时,
时, ![]() ,则
,则 ![]() ,
,
结合频率分布直方图可知: ![]() ,
,
∴ ![]() ;
;
(3)
由题意可知 ![]() 可取50,150,250,350,450,550.
可取50,150,250,350,450,550.
当 ![]() 时,
时, ![]() ,∴
,∴ ![]() ,
,
当 ![]() 时,
时, ![]() ,∴
,∴ ![]() ,
,
当 ![]() 时,
时, ![]() ,∴
,∴ ![]() ,
,
当 ![]() 时,
时, ![]() ,∴
,∴ ![]() ,
,
当 ![]() 时,
时, ![]() ,∴
,∴ ![]() ,
,
当 ![]() 时,
时, ![]() ,∴
,∴ ![]() ,
,
故 ![]() 的概率分布列为:
的概率分布列为:
| 25 | 75 | 140 | 220 | 310 | 410 |
| 0.1 | 0.2 | 0.3 | 0.2 | 0.15 | 0.05 |
所以随机变量 ![]() 的数学期望
的数学期望
![]() .
.
【解析】(1)分段计算,表示出y和x之间的关系;(2)根据y=260元计算出相对应的x的值为400,依据题意有P(x≤400)=0.8;P(x≤400)+P(400<x≤600)=0.2;(3)根据期望值进行计算即可。
【考点精析】解答此题的关键在于理解频率分布直方图的相关知识,掌握频率分布表和频率分布直方图,是对相同数据的两种不同表达方式.用紧凑的表格改变数据的排列方式和构成形式,可展示数据的分布情况.通过作图既可以从数据中提取信息,又可以利用图形传递信息.

【题目】为调查了解某省属师范大学师范类毕业生参加工作后,从事的工作与教育是否有关的情况,该校随机调查了该校80位性别不同的2016年师范类毕业大学生,得到具体数据如表:
与教育有关 | 与教育无关 | 合计 | |
男 | 30 | 10 | 40 |
女 | 35 | 5 | 40 |
合计 | 65 | 15 | 80 |
(1)能否在犯错误的概率不超过5%的前提下,认为“师范类毕业生从事与教育有关的工作与性别有关”? 参考公式: ![]() (n=a+b+c+d).
(n=a+b+c+d).
附表:
P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.023 | 6.635 |
(2)求这80位师范类毕业生从事与教育有关工作的频率;
(3)以(2)中的频率作为概率.该校近几年毕业的2000名师范类大学生中随机选取4名,记这4名毕业生从事与教育有关的人数为X,求X的数学期望E(X).