题目内容
【题目】如图1,![]() 是等边三角形,D.E分别是BC.AC上两点,且
是等边三角形,D.E分别是BC.AC上两点,且![]() ,
,![]() 与AD交于点H,链接CH.
与AD交于点H,链接CH.
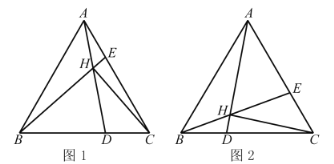
(1)当![]() 时,求
时,求![]() 的值;
的值;
(2)如图2,当![]() 时,
时,![]() __________;
__________;![]() __________.
__________.
【答案】(1)![]() ; (2)
; (2)![]() ;
;![]() .
.
【解析】
(1)根据题意可得![]() ,得出
,得出![]() ,证明
,证明![]() 四点共圆,连接
四点共圆,连接![]() ,由圆周角定理得出
,由圆周角定理得出![]() 得出
得出
![]() ,作
,作![]() 于
于![]() 则
则![]() ,得出
,得出![]() ,利用平行线的比例关系,结合
,利用平行线的比例关系,结合![]() 边角关系,即可得出结果;
边角关系,即可得出结果;
(2)同(1)得:![]() 四点共圆,连接
四点共圆,连接![]() ,由圆周角定理得出
,由圆周角定理得出![]() ,
,
![]() ,得出
,得出![]() ,得出
,得出![]() ,作
,作![]() 交
交![]() 于
于![]() ,则
,则![]() ,得出
,得出![]() ,与(1)同理,可得出结论.
,与(1)同理,可得出结论.
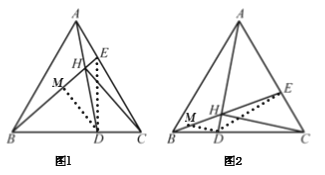
(1)![]() 是等边三角形,
是等边三角形,![]()
![]() ,
,
![]() ,
,
![]() ,
,
![]() 四点共圆,连接
四点共圆,连接![]() ,如图(1)所示,
,如图(1)所示,
则![]() ,
,
![]() ,
,
![]() ,作
,作![]() 于
于![]() ,
,
则![]() ,
,
![]() ,
,
设![]() ,则
,则![]() ,在
,在![]() 中,
中,
![]() ,
,
![]() ;
;
(2)同(1)得:![]() 四点共圆,连接
四点共圆,连接![]() ,
,
![]() ,
,
![]()
![]() ,
,![]() ,
,
作![]() 交
交![]() 于
于![]() ,则
,则![]() ,
,![]() ,
,
![]() ,设
,设![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
![]() .
.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案
相关题目
【题目】为了提高学生的身体素质,某校高一、高二两个年级共![]() 名学生同时参与了“我运动,我健康,我快乐”的跳绳、踢毽等系列体育健身活动.为了了解学生的运动状况,采用分层抽样的方法从高一、高二两个年级的学生中分别抽取
名学生同时参与了“我运动,我健康,我快乐”的跳绳、踢毽等系列体育健身活动.为了了解学生的运动状况,采用分层抽样的方法从高一、高二两个年级的学生中分别抽取![]() 名和
名和![]() 名学生进行测试.下表是高二年级的
名学生进行测试.下表是高二年级的![]() 名学生的测试数据(单位:个/分钟):
名学生的测试数据(单位:个/分钟):
学生编号 | 1 | 2 | 3 | 4 | 5 |
跳绳个数 | 179 | 181 | 168 | 177 | 183 |
踢毽个数 | 85 | 78 | 79 | 72 | 80 |
(1)求高一、高二两个年级各有多少人?
(2)设某学生跳绳![]() 个/分钟,踢毽
个/分钟,踢毽![]() 个/分钟.当
个/分钟.当![]() ,且
,且![]() 时,称该学生为“运动达人”.
时,称该学生为“运动达人”.
①从高二年级的学生中任选一人,试估计该学生为“运动达人”的概率;
②从高二年级抽出的上述![]() 名学生中,随机抽取
名学生中,随机抽取![]() 人,求抽取的
人,求抽取的![]() 名学生中为“span>运动达人”的人数
名学生中为“span>运动达人”的人数![]() 的分布列和数学期望.
的分布列和数学期望.