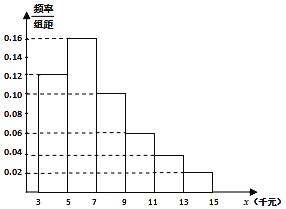
题目内容
【题目】如图,四棱柱ABCD-A1B1C1D1的底面为菱形,AA1⊥底面ABCD,∠BAD=120°,AB=2,E,F分别为CD,AA1的中点.
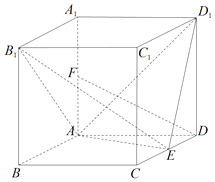
(Ⅰ)求证:DF∥平面B1AE;
(Ⅱ)若直线AD1与平面B1AE所成角的正弦值为![]() ,求AA1的长;
,求AA1的长;
(Ⅲ)在(Ⅱ)的条件下,求二面角B1-AE-D1的正弦值.
【答案】(Ⅰ)证明见解析(Ⅱ)2![]()
【解析】
(I)取AB1的中点G,连接FG,GE,证明四边形GEDF是平行四边形,可得DF![]() EG,故而DF
EG,故而DF![]() 平面B1AE;
平面B1AE;
(II)建立空间坐标系,求出平面B1AE的法向量![]() ,设AA1=t(t>0),令sinα=|cos<
,设AA1=t(t>0),令sinα=|cos<![]() ,
,![]() >|=
>|=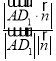 =
=![]() =
=![]() ,求出t;
,求出t;
(III)求出两半平面的法向量,计算法向量的夹角得出二面角的大小
(Ⅰ)证明:取AB1的中点G,连接FG,GE,
∵![]() ,FG
,FG![]() A1B1,
A1B1,![]() ,DE
,DE![]() A1B1,
A1B1,
∴FG=DE,FG![]() DE,
DE,
∴GEDF是平行四边形,
∴DF![]() EG,
EG,
又DF平面B1AE,EG平面B1AE,
∴DF![]() 平面B1AE
平面B1AE
解:(Ⅱ)在菱形ABCD中,
∵∠BAD=120°,
∴∠ADC=60°,
∴△ACD是等边三角形,
∴AE⊥CD,
∴AE⊥AB,
又AA1⊥平面ABCD,
∴AA1⊥AB,AA1⊥AE,
以A为坐标原点,建立如图所示的空间直角坐标系,
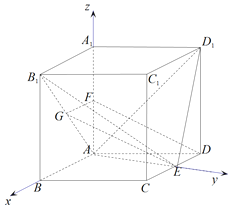
设AA1=t(t>0),
则![]() ,
,
∴![]() ,
,![]() ,
,
设平面B1AE的法向量![]() =(x,y,z),则
=(x,y,z),则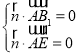 ,即
,即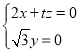 ,
,
不妨取z=-2,得![]() =(t,0,-2),
=(t,0,-2),
设直线AD1与平面B1AE所成的角为α,
则sinα=|cos<![]() ,
,![]() >|=
>|=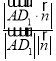 =
=![]() =
=![]() .
.
解得t=2,即AA1的长为2.
(Ⅲ)设平面D1AE的法向量![]() =(x,y,z),
=(x,y,z),
∵![]() ,
,
∴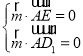 ,即
,即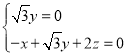 ,
,
不妨取z=1,得![]() =(2,0,1),
=(2,0,1),
设二面角B1-AE-D1的平面角为θ,则|cosθ|=|cos<![]() >|=
>|=![]() =
=![]() =
=![]()
∴![]() ,即二面角B1-AE-D1的正弦值为
,即二面角B1-AE-D1的正弦值为![]()

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目