题目内容
【题目】已知函数f（x）=（|x|﹣b）2+c，函数g（x）=x+m．
（1）当b=2，m=﹣4时，f（x）≥g（x）恒成立，求实数c的取值范围；
（2）当c=﹣3，m=﹣2时，方程f（x）=g（x）有四个不同的解，求实数b的取值范围．
【答案】（1）c≥﹣
；（2）b≥1且1＜b＜
.
【解析】
试题（1）代入b=2，m=﹣4，
，去绝对值变形为c≥x﹣4﹣（|x|﹣2）2=
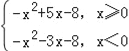，只需求得右边分段函数的最大值．（2）代入c=﹣3，m=﹣2
，得（|x|﹣b）2=x+1有四个不同的解，所以（x﹣b）2=x+1（x≥0）有两个不同解且
（x+b）2=x+1（x＜0）也有两个不同解，两个二次函数均在各自区间上有两个实数解，由根的分布，可解出b的范围．
试题解析：（1）∵当b=2，m=﹣4时，f（x）≥g（x）恒成立，
∴c≥x﹣4﹣（|x|﹣2）2=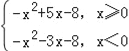，由二次函数的性质得c≥﹣．
（2）（|x|﹣b）2﹣3=x﹣2，即（|x|﹣b）2=x+1有四个不同的解，
∴（x﹣b）2=x+1（x≥0）有两个不同解以及（x+b）2=x+1（x＜0）也有两个不同解，
由根的分布得b≥1且1＜b＜，
∴1＜b＜．
练习册系列答案
名校课堂系列答案
相关题目
