Question

【题目】已知函数f（x）是定义在R上的奇函数，且当x≤0时，f（x）=x2+2x．

（1）求函数f（x）（x∈R）的解析式；
（2）现已画出函数f（x）在y轴左侧的图象，如图所示，请补全完整函数f（x）的图象；
（3）求使f（x）＞0的实数x的取值集合．

Answer 1

【答案】
（1）解：设x＞0，则﹣x＜0，

∴f（﹣x）=（﹣x）2+2×（﹣x）=x2﹣2x，

∵函数f（x）是定义在R上的奇函数，

∴f（x）=﹣f（﹣x）=﹣x2+2x（x＞0），

∴

（2）解：函数的图象如图所示：

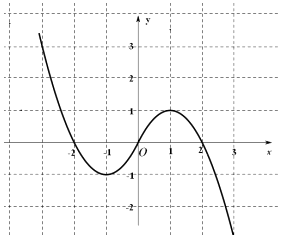
（3）解：方程f（x）=0的根是x1=﹣2，x2=0，x3=2，

由函数的图象可知不等式f（x）＞0的解集为{x|x＜﹣2或0＜x＜2}

【解析】（1）根据f（-x）=-f（x）求出当x0时函数f（x）的解析式；（2）根据奇函数图象的对称性；（3）结合（2）的图象即可求解.
【考点精析】认真审题，首先需要了解函数的图象(函数的图像是由直角坐标系中的一系列点组成；图像上每一点坐标（x，y）代表了函数的一对对应值，他的横坐标x表示自变量的某个值，纵坐标y表示与它对应的函数值)．