题目内容
3．函数y=$\sqrt{\frac{x+1}{x-1}}$的定义域为{x|x＞1或x≤-1}．分析 根据函数的解析式和求定义域的法则列出不等式组，求出不等式的解集，用集合或区间的形式表示出来．
解答 解：要使函数有意义，则$\left\{\begin{array}{l}{x-1≠0}\\{\frac{x+1}{x-1}≥0}\end{array}\right.$，
解得x＞1或x≤-1，
所以函数的定义域是{x|x＞1或x≤-1}，
故答案为：{x|x＞1或x≤-1}．
点评 本题考查函数的定义域，掌握函数定义域的法则是解题的关键，属于基础题．
练习册系列答案
阳光课堂课时作业系列答案
相关题目
如图，点A，B是单位圆上的两点，A，B点分别在第一、二象限，点C是圆与x轴正半轴的交点，△AOB是正三角形，记∠COA=α．
8．在对人们的休闲方式的一次调查中，共调查了120人，其中女性65人，男性55人．女性中有40人主要的休闲方式是看电视，另外25人主要的休闲方式是运动；男性中有20人主要的休闲方式是看电视，另外35人主要的休闲方式是运动．${K^2}=\frac{{n{{（{ab-bc}）}^2}}}{{（{a+b}）（{c+d}）（{a+c}）（{b+d}）}}$
其中n=a+b+c+d
（1）根据以上数据建立一个2×2的列联表；
（2）能够以多大的把握认为性别与休闲方式有关系，为什么？
其中n=a+b+c+d
| P（K2≥k） | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
（2）能够以多大的把握认为性别与休闲方式有关系，为什么？
15．
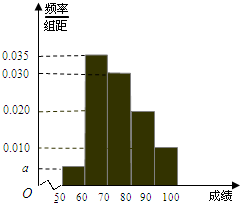某校100名学生期中考试数学成绩的频率分布直方图如图，其中成绩分组区间如下：
（1）求图中a的值；
（2）根据频率分布直方图，估计这100名学生期中考试数学成绩的平均数．
某校100名学生期中考试数学成绩的频率分布直方图如图，其中成绩分组区间如下：| 组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
| 分组 | [50，60） | [60，70） | [70，80） | [80，90） | [90，100] |
（2）根据频率分布直方图，估计这100名学生期中考试数学成绩的平均数．