题目内容
12.已知数列{an}的前n项和Sn,a1=-$\frac{2}{3}$,Sn+$\frac{1}{S_n}+2={a_n}$(n≥2).(1)计算S1,S2,S3,猜想Sn的表达式并用数学归纳法证明;
(2)设bn=$\frac{S_n}{{{n^2}+n}}$,数列的{bn}的前n项和为Tn,求证:Tn>-$\frac{3}{4}$.
分析 (1)利用已知条件计算S1,S2,S3,猜想Sn的表达式,然后用数学归纳法证明步骤证明即可;
(2)化简bn=$\frac{S_n}{{{n^2}+n}}$,利用裂项法求解数列的{bn}的前n项和为Tn,即可证明Tn>-$\frac{3}{4}$.
解答 (本小题满分12分)
解:(1)因为an=Sn-Sn-1(n≥2),所以${S_n}+\frac{1}{S_n}+2={S_n}-{S_{n-1}}$,由此整理得${S_n}=-\frac{1}{{2+{S_{n-1}}}}$,于是有:${S_1}=-\frac{2}{3},{S_2}=-\frac{3}{4},{S_3}=-\frac{4}{5}$,
猜想:${S_n}=-\frac{n+1}{n+2}$
证明:①当n=1时,${S_1}=-\frac{2}{3}$,猜想成立.
②假设n=k时猜想成立,即${S_k}=-\frac{k+1}{k+2}$,
那么${S_{k+1}}=-\frac{1}{{2+{S_k}}}=-\frac{1}{{2-\frac{k+1}{k+2}}}=-\frac{k+2}{k+3}=-\frac{k+1}{(k+1)+2}$,
所以当n=k+1时猜想成立,由①②可知,猜想对任何n∈N*都成立.(6分)
(2)由(1)${b_n}=-\frac{1}{n(n+2)}=-\frac{1}{2}(\frac{1}{n}-\frac{1}{n+2})$,于是:${T_n}=-\frac{1}{2}[(1+\frac{1}{2}+\frac{1}{3}+…+\frac{1}{n})-(\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+…+\frac{1}{n+2})]=-\frac{1}{2}(\frac{3}{2}-\frac{1}{n+1}-\frac{1}{n+2})$,
又因为$\frac{3}{2}-\frac{1}{n+1}-\frac{1}{n+2}$$<\frac{3}{2}$,
所以${T_n}>-\frac{3}{4}$.(12分)
点评 本小题主要考查利用数学归纳法解决有关于数列的问题,虽存在着一定的难度,但是考试大纲规定考查内容,属于一道中档题,对考生的运算求解能力,化归与转化能力提出一定要求.

 名校课堂系列答案
名校课堂系列答案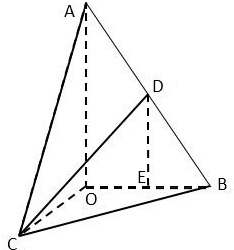 如图,已知正三角形ABC的边长为6,将△ABC沿BC边上的高线AO折起,使BC=3$\sqrt{2}$,得到三棱锥A-BOC.动点D在边AB上.
如图,已知正三角形ABC的边长为6,将△ABC沿BC边上的高线AO折起,使BC=3$\sqrt{2}$,得到三棱锥A-BOC.动点D在边AB上.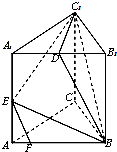 在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,D为棱A1B1的中点,E为AA1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB.
在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,D为棱A1B1的中点,E为AA1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB. 如图,已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是
如图,已知四边形ABCD满足AD∥BC,BA=AD=DC=$\frac{1}{2}$BC=a,E是 如图,已知PE为圆eO的切线,切点为E,割线PBA交eO于A、B两点,C为AE上一点,且∠CPE=∠CPA.
如图,已知PE为圆eO的切线,切点为E,割线PBA交eO于A、B两点,C为AE上一点,且∠CPE=∠CPA.