题目内容
3.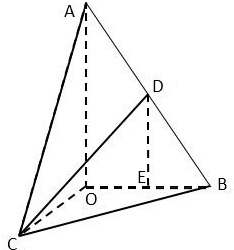 如图,已知正三角形ABC的边长为6,将△ABC沿BC边上的高线AO折起,使BC=3$\sqrt{2}$,得到三棱锥A-BOC.动点D在边AB上.
如图,已知正三角形ABC的边长为6,将△ABC沿BC边上的高线AO折起,使BC=3$\sqrt{2}$,得到三棱锥A-BOC.动点D在边AB上.(1)求证:OC⊥平面AOB;
(2)当点D为AB的中点时,求异面直线AO、CD所成角的正切值;
(3)求当直线CD与平面AOB所成角最大时的正切值.
分析 (1)对比折叠前后便可得出,AO⊥平面BOC,从而OC⊥AO,并且可说明△BOC为直角三角形,OC⊥OD,从而得到OC⊥平面AOB;
(2)根据上面可分别以OC,OB,OA三直线为x,y,z轴,建立空间直角坐标系,从而求出向量$\overrightarrow{AO}$,$\overrightarrow{CD}$的坐标.设异面直线AO、CD所成角为θ,由cos$θ=|cos<\overrightarrow{AO},\overrightarrow{CD}>|$即可求出cosθ,再求出sinθ,从而求出tanθ;
(3)根据条件并结合图形可设D($0,3-\frac{\sqrt{3}}{3}z,z$),并且说明$\overrightarrow{OC}$是平面AOB的法向量,设直线CD与平面AOB所成角为α,从而根据sin$α=|cos<\overrightarrow{CD},\overrightarrow{OC}>|$即可求得α最大时sinα值,从而求出cosα,tanα.
解答 解:(1)证明:根据条件,AO⊥OB,AO⊥OC,OB∩OC=O;
∴AO⊥底面BCO,OC?平面BCO;
∴AO⊥OC,即OC⊥AO;
又OB=OC=3,BC=3$\sqrt{2}$;
∴OB2+OC2=BC2;
∴OC⊥OB,AO∩OB=O;
∴OC⊥平面AOB;
∴OC,OB,OA三直线两两垂直,分别以这三直线为x,y,z轴,建立如图所示空间直角坐标系,则: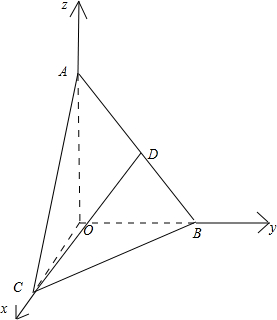 O(0,0,0),A(0,0,3$\sqrt{3}$),B(0,3,0),C(3,0,0);
O(0,0,0),A(0,0,3$\sqrt{3}$),B(0,3,0),C(3,0,0);
D为AB中点,∴D(0,$\frac{3}{2},\frac{3\sqrt{3}}{2}$);
∴$\overrightarrow{AO}=(0,0,-3\sqrt{3})$,$\overrightarrow{CD}=(-3,\frac{3}{2},\frac{3\sqrt{3}}{2})$;
设异面直线AO,CD所成角为θ,则cosθ=|cos$<\overrightarrow{AO},\overrightarrow{CD}>$|=$\frac{\frac{27}{2}}{3\sqrt{3}•3\sqrt{2}}=\frac{\sqrt{6}}{4}$;
∴$sinθ=\frac{\sqrt{10}}{4}$,tan$θ=\frac{\sqrt{10}}{\sqrt{6}}=\frac{\sqrt{15}}{3}$;
即异面直线AO、CD所成角的正切值为$\frac{\sqrt{15}}{3}$;
(3)由(1)知,$\overrightarrow{OC}=(3,0,0)$为平面AOB的法向量,设直线CD与平面AOB所成角为α,D(0,$3-\frac{\sqrt{3}}{3}z,z$),($0≤z≤3\sqrt{3}$),则:
sin$α=|cos<\overrightarrow{OC},\overrightarrow{CD}>|$=$\frac{9}{3•\sqrt{9+(3-\frac{\sqrt{3}}{3}z)^{2}+{z}^{2}}}$=$\frac{3}{\sqrt{\frac{4}{3}(z-\frac{3\sqrt{3}}{4})^{2}+\frac{63}{4}}}$;
∴$z=\frac{3\sqrt{3}}{4}$时,sinα取最大值$\frac{2\sqrt{7}}{7}$,此时α最大;
∴此时cosα=$\frac{\sqrt{21}}{7}$,tanα=$\frac{2\sqrt{3}}{3}$;
∴当直线CD与平面AOB所成角最大时的正切值为$\frac{2\sqrt{3}}{3}$.
点评 考查对折叠前后图形的认识,线面垂直的判定,线面垂直的性质,以及通过建立空间直角坐标系,利用空间向量求线线角及线面角的方法,平面法向量的概念,直线和平面所成角与直线的方向向量和平面法向量夹角的关系,以及清楚异面直线所成角和线面角的范围.

| A. | y=($\frac{1}{2}$)-x | B. | y=sinx2 | C. | y=x|x| | D. | y=ln|x| |
| A. | 45° | B. | 135° | C. | -45° | D. | 120° |
| A. | (0,3) | B. | [2,3) | C. | (2,3) | D. | [3,+∞) |
| A. | ?x≥0,|x0|+x0<0 | B. | ?x<0,|x|+x≥0 | C. | ?x0≥0,|x0|+x0<0 | D. | ?x0<0,|x|+x≥0 |
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{2}$ |



