题目内容
7.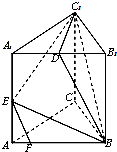 在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,D为棱A1B1的中点,E为AA1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB.
在三棱柱ABC-A1B1C1中,AB=BC=CA=AA1=2,侧棱AA1⊥平面ABC,D为棱A1B1的中点,E为AA1的中点,点F在棱AB上,且AF=$\frac{1}{4}$AB.(1)求证:EF∥平面BC1D;
(2)求点D到平面EBC1的距离.
分析 (1)直接利用直线与平面平行的判定定理证明EF∥平面BC1D.
(2)证明C1D⊥平面ABB1A1,求出棱锥的底面面积,然后求解即可.
解答 解:(1)证明:由$\frac{{D{B_1}}}{{B{B_1}}}=\frac{AF}{AE}=\frac{1}{2}$,可知EF∥BD,$\left.\begin{array}{l}EF∥BD\\ BD?平面B{C_1}D\end{array}\right\}⇒EF∥平面B{C_1}D$.(6分)
(2)由题可知${S_{△EBD}}={S_{AB{B_1}{A_1}}}-{S_{△{A_1}DE}}-{S_{△ABE}}-{S_{△BD{B_1}}}=\frac{3}{2}$.$\left.\begin{array}{l}\left.\begin{array}{l}{A_1}A⊥平面{A_1}{B_1}{C_1}\\{C_1}D?平面{A_1}{B_1}{C_1}\end{array}\right\}⇒{A_1}A⊥{C_1}D\\{C_1}D⊥{A_1}{B_1}\end{array}\right\}⇒{C_1}D⊥平面AB{B_1}{A_1}$
则${V_{{C_1}-EBD}}=\frac{1}{3}{S_{△EBD}}•{C_1}D=\frac{{\sqrt{3}}}{2}$,△EBC1中,$EC=\sqrt{5}$,$EB=\sqrt{5}$,$B{C_1}=2\sqrt{2}$,
则${S_{△EB{C_1}}}=\sqrt{6}$${V_{{C_1}-EBD}}=\frac{1}{3}{S_{△EB{C_1}}}•h=\frac{1}{3}\sqrt{6}•h=\frac{{\sqrt{3}}}{2}$,则$h=\frac{{3\sqrt{2}}}{4}$.(12分)
点评 本小题主要考查立体几何的相关知识,具体涉及到线面的平行关系、空间点面距离的求法.本小题对考生的空间想象能力与运算求解能力有较高要求.

 应用题作业本系列答案
应用题作业本系列答案| A. | 45° | B. | 135° | C. | -45° | D. | 120° |
| A. | ?x≥0,|x0|+x0<0 | B. | ?x<0,|x|+x≥0 | C. | ?x0≥0,|x0|+x0<0 | D. | ?x0<0,|x|+x≥0 |
| A. | $\sqrt{2}$ | B. | 1 | C. | 2 | D. | $\sqrt{3}$ |
| A. | 8 | B. | 15 | C. | 16 | D. | 32 |