题目内容
在四棱锥中S-ABCD中，底面ABCD是梯形，AD∥BC，AB=BC=
AD，E为AD中点，且SA⊥底面ABCD．证明：BE∥面SCD．
| 1 |
| 2 |
考点：直线与平面平行的判定
专题：空间位置关系与距离
分析：根据线面垂直的判定定理即可得到结论．
解答：
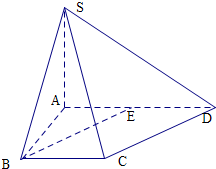解：∵底面ABCD是梯形，AD∥BC，AB=BC=
AD，E为AD中点，
∴DE∥BC，且DE=BC，
则四边形BCDE为平行四边形，
则BE∥CD，
∵BE?平面SCD，CE?平面SCD，
∴BE∥面SCD
解：∵底面ABCD是梯形，AD∥BC，AB=BC=| 1 |
| 2 |
∴DE∥BC，且DE=BC，
则四边形BCDE为平行四边形，
则BE∥CD，
∵BE?平面SCD，CE?平面SCD，
∴BE∥面SCD
点评：本题主要考查线面平行的判定，比较基础．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
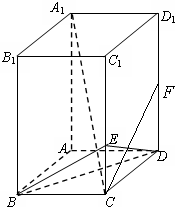如图所示，在长方体ABCD-A1B1C1D1中，AB=BC=2，BB1=4，E是棱CC1上的点，且CE=1；F是DD1中点礼堂第一排有a个座位，后面每一排比前一排多一个座位，则第n排的座位是（ ）
| A、n+1 |
| B、a+（n+1） |
| C、a+n |
| D、a+（n-1） |