题目内容
已知定义域在R上的函数y=f(x)是减函数,则f(a-2)-f(4-a2)<0,求a的取值范围.
考点:函数单调性的性质
专题:函数的性质及应用
分析:根据函数y=f(x)在定义域R上是减函数,则能推出不等式a-2>4-a2,从而求出a的取值范围.
解答:
解:因为y=f(x)在定义域R上是减函数,f(a-2)-f(4-a2)<0,可得f(a-2)<f(4-a2),
使用由减函数的性质可知a-2>4-a2,解得a<-3或a>2.所以a的取值范围是(-∞,-3)∪(2,+∞).
故答案为:(-∞,-3)∪(2,+∞).
使用由减函数的性质可知a-2>4-a2,解得a<-3或a>2.所以a的取值范围是(-∞,-3)∪(2,+∞).
故答案为:(-∞,-3)∪(2,+∞).
点评:本题考查了函数的单调性的应用,属于基础题型.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
已知P是以F1,F2为焦点的椭圆
+
=1(a>b>0)上的任意一点,若∠PF1F2=α,∠PF2F1=β,且cosα=
,sin(α+β)=
,则此椭圆的离心率可以为( )
| x2 |
| a2 |
| y2 |
| b2 |
| ||
| 5 |
| 3 |
| 5 |
A、
| ||||||||
B、
| ||||||||
C、
| ||||||||
D、
|
礼堂第一排有a个座位,后面每一排比前一排多一个座位,则第n排的座位是( )
| A、n+1 |
| B、a+(n+1) |
| C、a+n |
| D、a+(n-1) |
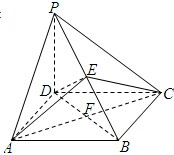 如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=6,BD=6
如图,在四棱锥P-ABCD中,PD⊥平面ABCD,四边形ABCD是菱形,AC=6,BD=6