题目内容
【题目】已知正方体![]() ,过对角线
,过对角线![]() 作平面
作平面![]() 交棱
交棱![]() 于点
于点![]() ,交棱
,交棱![]() 于点
于点![]() ,下列不正确的是( )
,下列不正确的是( )
A.平面![]() 分正方体所得两部分的体积相等;
分正方体所得两部分的体积相等;
B.四边形![]() 一定是平行四边形;
一定是平行四边形;
C.平面![]() 与平面
与平面![]() 不可能垂直;
不可能垂直;
D.四边形![]() 的面积有最大值.
的面积有最大值.
【答案】C
【解析】
利用正方体的对称性即可判断A正确; 由平行平面的性质可判断B正确;当![]() 为棱中点时,通过线面垂直可得面面垂直,判断C错误;结合异面直线距离说明四边形
为棱中点时,通过线面垂直可得面面垂直,判断C错误;结合异面直线距离说明四边形![]() 的面积最大值取法,判断D正确.
的面积最大值取法,判断D正确.
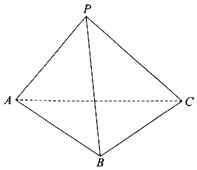
作出草图,如下图:

对于A:由正方体的对称性可知,平面![]() 分正方体所得两部分的体积相等,故A正确;
分正方体所得两部分的体积相等,故A正确;
对于B:因为平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
平面![]() 平面
平面![]() ,∴
,∴![]() .
.
同理可证:![]() ,故四边形
,故四边形![]() 一定是平行四边形,故B正确;
一定是平行四边形,故B正确;
对于C:当![]() 为棱中点时,
为棱中点时,![]() 平面
平面![]() ,又因为
,又因为![]() 平面
平面![]() ,
,
所以平面![]() 平面
平面![]() ,故C不正确;
,故C不正确;
对于D:由B得四边形![]() 一定是平行四边形,所以四边形
一定是平行四边形,所以四边形![]() 的面积等于三角形
的面积等于三角形![]() 面积的两倍,而
面积的两倍,而![]() 为定值,所以当
为定值,所以当![]() 到直线
到直线![]() 距离最大时,三角形
距离最大时,三角形![]() 面积取最大值,因为
面积取最大值,因为![]() 为棱
为棱![]() 中点时,
中点时, ![]() 到直线
到直线![]() 距离恰为异面直线
距离恰为异面直线![]() 距离,即为最小值,因此当E与A重合或
距离,即为最小值,因此当E与A重合或![]() 重合时,三角形
重合时,三角形![]() 面积取最大值,即四边形
面积取最大值,即四边形![]() 的面积即取最大值,故D正确.
的面积即取最大值,故D正确.
故选:C.

练习册系列答案
 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案
相关题目