Question

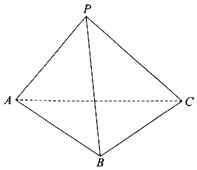
【题目】如图，在三棱锥P-ABC中，平面PAC⊥平面ABC，∠PAC=∠BAC=60°，AC=4，AP=3，AB=2．

（1）求三棱锥P-ABC的体积；

（2）求点C到平面PAB距离．

Answer 1

【答案】（1）3； （2）.

【解析】

（1）过P作PH⊥AC交AC于一点H，可证PH⊥平面ABC，计算PH和△ABC的面积，代入体积公式计算棱锥的体积；

（2）依次计算AH，BH，PB，利用余弦定理计算∠PAB，得出△PAB的面积，根据VP-ABC=VC-PAB列方程计算C到平面PAB的距离．

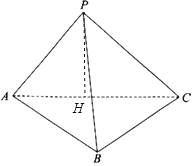
（1）过P作PH⊥AC交AC于一点H，

∵平面PAC⊥平面ABC，平面PAC∩平面ABC=AC，PH平面PAC，

∴PH⊥平面ABC．

在△PAC中，∠PAC=60°，PA=3，则PH=PAsin∠PAC=，AH=PAcos∠PAC=．

∵△ABC的面积S△ABC===2．

∴四面体P-ABC体积VP-ABC===3．

（2）连接BH．

在△ABH中，由余弦定理可得：BH2=AH2+AB2-2AHABcos∠BAC=+4-2×=，

∴PB2=PH2+BH2=+=10，∴PB=．

在△PAB中，由余弦定理得：cos∠PAB===，∴sin∠PAB=．

∴△PAB的面积S△PAB===．

设C点到平面PAB距离为h，则VC-PAB=S△PABh=3，

即=3．解得h=．

∴C点到平面PAB距离为．