题目内容
【题目】函数f(x)=Asin(ωx+φ)(A>0,|φ|< ![]() )其中的图象如图所示,为了得到g(x)=cos(2x﹣
)其中的图象如图所示,为了得到g(x)=cos(2x﹣ ![]() )的图象,只需将f(x)的图象( )
)的图象,只需将f(x)的图象( ) 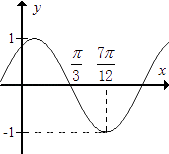
A.向左平移 ![]() 个单位
个单位
B.向右平移 ![]() 个单位
个单位
C.向左平移 ![]() 个单位
个单位
D.向右平移 ![]() 个单位
个单位
【答案】D
【解析】解:∵由函数图象可得:A的值为1,周期T=4×( ![]() ﹣
﹣ ![]() )=π,
)=π,
∴ω= ![]() =
= ![]() =2,
=2,
又函数的图象的第二个点是( ![]() ,0),
,0),
∴2× ![]() +φ=π,
+φ=π,
于是φ= ![]() ,则f(x)=sin(2x+
,则f(x)=sin(2x+ ![]() )=sin[2(x+
)=sin[2(x+ ![]() )],
)],
∵g(x)=cos(2x﹣ ![]() )=sin2x,
)=sin2x,
∴为了得到g(x)=cos(2x﹣ ![]() )的图象,只需将f(x)的图象向右平移
)的图象,只需将f(x)的图象向右平移 ![]() 个单位即可.
个单位即可.
故选:D.
【考点精析】关于本题考查的函数y=Asin(ωx+φ)的图象变换,需要了解图象上所有点向左(右)平移![]() 个单位长度,得到函数
个单位长度,得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的横坐标伸长(缩短)到原来的
的图象上所有点的横坐标伸长(缩短)到原来的![]() 倍(纵坐标不变),得到函数
倍(纵坐标不变),得到函数![]() 的图象;再将函数
的图象;再将函数![]() 的图象上所有点的纵坐标伸长(缩短)到原来的
的图象上所有点的纵坐标伸长(缩短)到原来的![]() 倍(横坐标不变),得到函数
倍(横坐标不变),得到函数![]() 的图象才能得出正确答案.
的图象才能得出正确答案.

练习册系列答案
相关题目
【题目】某学校为倡导全体学生为特困学生捐款,举行“一元钱,一片心,诚信用水”活动,学生在购水处每领取一瓶矿泉水,便自觉向捐款箱中至少投入一元钱.现统计了连续5天的售出和收益情况,如表:
售出水量x(单位:箱) | 7 | 6 | 6 | 5 | 6 |
收益y(单位:元) | 165 | 142 | 148 | 125 | 150 |
(1)求y关于x的线性回归方程;
(2)预测售出8箱水的收益是多少元?
附:回归直线的斜率和截距的最小二乘法估计公式分别为: ![]() =
= 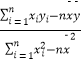 ,
, ![]() =
= ![]() ﹣
﹣ ![]()
![]() ,
,
参考数据:7×165+6×142+6×148+5×125+6×150=4420.