ћвƒњƒЏ»Ё
°Њћвƒњ°њ“љ…ъµƒ„®“µƒ№Ѕ¶≤ќ э![]() њ…”––ІЇвЅњ“љ…ъµƒ„џЇѕƒ№Ѕ¶£ђ
њ…”––ІЇвЅњ“љ…ъµƒ„џЇѕƒ№Ѕ¶£ђ![]() ‘љіу£ђ„џЇѕƒ№Ѕ¶‘љ«њ£ђ≤Ґєжґ®: ƒ№Ѕ¶≤ќ э
‘љіу£ђ„џЇѕƒ№Ѕ¶‘љ«њ£ђ≤Ґєжґ®: ƒ№Ѕ¶≤ќ э![]() ≤ї…ў”Џ30≥∆ќ™ЇѕЄс£ђ≤ї…ў”Џ50≥∆ќ™”≈–г£Ѓƒ≥ –ќј…ъє№јн≤њ√≈Ћжїъ≥й»°300√ы“љ…ъљш––„®“µƒ№Ѕ¶≤ќ эњЉЇЋ£ђµ√µљ»зЌЉЋщ Њµƒƒ№Ѕ¶
≤ї…ў”Џ30≥∆ќ™ЇѕЄс£ђ≤ї…ў”Џ50≥∆ќ™”≈–г£Ѓƒ≥ –ќј…ъє№јн≤њ√≈Ћжїъ≥й»°300√ы“љ…ъљш––„®“µƒ№Ѕ¶≤ќ эњЉЇЋ£ђµ√µљ»зЌЉЋщ Њµƒƒ№Ѕ¶![]() µƒ∆µ¬ Ј÷≤Љ÷±ЈљЌЉ:
µƒ∆µ¬ Ј÷≤Љ÷±ЈљЌЉ:
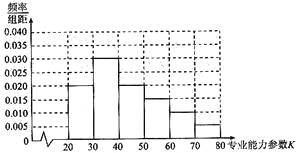
£®Ґс£©«у≥ц’вЄц—щ±ЊµƒЇѕЄс¬ °Ґ”≈–г¬ £ї
£®Ґт£©ѕ÷”√Ј÷≤г≥й—щµƒЈљЈ®і”÷–≥й≥ц“їЄц—щ±Њ»ЁЅњќ™20µƒ—щ±Њ£ђ‘ўі”’в20√ы“љ…ъ÷–Ћжїъ—°≥ц2√ы£Ѓ
Ґў«у’в2√ы“љ…ъµƒƒ№Ѕ¶≤ќ э![]() ќ™Ќђ“ї„йµƒЄ≈¬ £ї
ќ™Ќђ“ї„йµƒЄ≈¬ £ї
ҐЏ…и’в2√ы“љ…ъ÷–ƒ№Ѕ¶≤ќ э![]() ќ™”≈–гµƒ»Ћ эќ™
ќ™”≈–гµƒ»Ћ эќ™![]() £ђ«уЋжїъ±дЅњ
£ђ«уЋжїъ±дЅњ![]() µƒЈ÷≤ЉЅ–ЇЌ∆ЏЌы£Ѓ
µƒЈ÷≤ЉЅ–ЇЌ∆ЏЌы£Ѓ
°Њір∞Є°њ£®1£©Єч„йµƒ∆µ¬ “јіќќ™0.2£ђ0.3£ђ0.2£ђ0.15£ђ0.1£ђ0.05£ђ
![]() ’вЄц—щ±ЊµƒЇѕЄс¬ ќ™1£≠0.2=0.8£ђ”≈–г¬ ќ™0.15+0.1+0.05=0.3°£
’вЄц—щ±ЊµƒЇѕЄс¬ ќ™1£≠0.2=0.8£ђ”≈–г¬ ќ™0.15+0.1+0.05=0.3°£
ƒ№Ѕ¶≤ќ эKµƒ∆љЊщ÷µќ™25°Ѕ0.2+35°Ѕ0.3+45°Ѕ0.2+55°Ѕ0.15+65°Ѕ0.1+75°Ѕ0.05="43."
£®2£©Ј÷≤ЉЅ–ќ™
X | 0 | 1 | 2 |
P |
|
|
|
![]() µƒ∆ЏЌы÷µ
µƒ∆ЏЌы÷µ![]() .
.
°Њљвќц°њ ‘ћвЈ÷ќц£Ї£®1£©”…∆µ¬ Ј÷≤Љ÷±ЈљЌЉ£ђЇѕЄс¬ «£Ї ![]()
”≈–г¬ «£Ї ![]()
£®2£©”…∆µ¬ Ј÷≤Љ÷±ЈљЌЉ£ђ«у≥ц’в20√ы“љ…ъ÷–£ђЄчґќ»Ћ эЈ÷±рќ™4»Ћ£ђ6»Ћ£ђ4»Ћ£ђ3»Ћ£ђ2»Ћ£ђ1»Ћ
Ґў”…є≈µдЄ≈–Ќ«у≥ц
ҐЏ”≈–гµƒ»Ћ эќ™£Ї3+2+1£љ6»Ћ£ђ ![]() “„µ√Ј÷≤ЉЅ–£ђ‘т∆ЏЌыњ…«у °≠
“„µ√Ј÷≤ЉЅ–£ђ‘т∆ЏЌыњ…«у °≠
‘ћвљвќц£Ї£®1£©ЇѕЄс¬ «£Ї ![]()
”≈–г¬ «£Ї ![]()
£®2£©”…ћв“в÷™£ђ’в20√ы“љ…ъ÷–£ђ[20£ђ30]”–4»Ћ£ђ[30£ђ40]”–6»Ћ£ђ[40£ђ50]”–4»Ћ£ђ[50£ђ60]”–3»Ћ£ђ[60£ђ70]”–2»Ћ£ђ[70£ђ80]”–1»Ћ
Ґў![]()
ҐЏ”≈–гµƒ»Ћ эќ™£Ї3+2+1£љ6»Ћ
![]()
![]() £ђ
£ђ ![]()
![]() µƒЈ÷≤ЉЅ– «£Ї
µƒЈ÷≤ЉЅ– «£Ї
| 0 | 1 | 2 |
|
|
|
|
є ![]() µƒ∆ЏЌы «
µƒ∆ЏЌы «![]() °≠
°≠

 —Іґш”≈ѕќљ”љћ≤ƒƒѕЊ©іу—І≥ц∞ж…зѕµЅ–ір∞Є
—Іґш”≈ѕќљ”љћ≤ƒƒѕЊ©іу—І≥ц∞ж…зѕµЅ–ір∞Є –°—Іњќћ√„ч“µѕµЅ–ір∞Є
–°—Іњќћ√„ч“µѕµЅ–ір∞Є