题目内容
11.若关于x的方程$\sqrt{3}$sinx+|cosx|+a=0在区间[0,2π]内有四个不同的解分别为x1,x2,x3,x4,则x1+x2+x3+x4的值为2π.分析 分类讨论,化简f(x)=$\sqrt{3}$sinx+|cosx|的解析式,由题意可得,f(x)的图象和直线y=-a在区间[0,2π]内有四个不同的交点,再利用正弦函数的图象的对称性,求得x1+x2+x3+x4的值.
解答 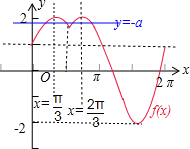 解:由题意可得函数f(x)=$\sqrt{3}$sinx+|cosx|=$\left\{\begin{array}{l}{2sin(x+\frac{π}{6}),x∈[0,\frac{π}{2}]}\\{2sin(x-\frac{π}{6}),x∈(\frac{π}{2},\frac{3π}{2}]}\\{2sin(x+\frac{π}{6}),x∈(\frac{3π}{2},2π]}\end{array}\right.$ 的图象
解:由题意可得函数f(x)=$\sqrt{3}$sinx+|cosx|=$\left\{\begin{array}{l}{2sin(x+\frac{π}{6}),x∈[0,\frac{π}{2}]}\\{2sin(x-\frac{π}{6}),x∈(\frac{π}{2},\frac{3π}{2}]}\\{2sin(x+\frac{π}{6}),x∈(\frac{3π}{2},2π]}\end{array}\right.$ 的图象
和直线y=-a在区间[0,2π]内有四个不同的交点,1<-a<2,即-2<a<-1.
故x1+x2 =2×$\frac{π}{3}$=$\frac{2π}{3}$,x3+x4 =2×$\frac{2π}{3}$=$\frac{4π}{3}$,
∴x1+x2+x3+x4=$\frac{2π}{3}$+$\frac{4π}{3}$2π,
故答案为:2π.
点评 本题主要考查两角和差的正弦公式,函数的零点和方程根的关系,正弦函数的图象的对称性,体现了转化、分类讨论的数学思想,属于中档题.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案 英才计划期末调研系列答案
英才计划期末调研系列答案
相关题目
6.某厂大量生产一种小零件,经抽样检验知道其次品率是1%,现把这种零件中6件装成一盒,那么该盒中恰好含一件次品的概率是( )
| A. | ($\frac{99}{100}$)2 | B. | 0.01 | ||
| C. | C${\;}_{6}^{1}$$\frac{1}{100}$•(1-$\frac{1}{100}$)5 | D. | C${\;}_{6}^{2}$($\frac{1}{100}$)2•(1-$\frac{1}{100}$)4 |
