题目内容
已知函数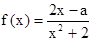 (x∈R)在区间[-1,1]上是增函数
(x∈R)在区间[-1,1]上是增函数
(Ⅰ)求实数a的值所组成的集合A
(Ⅱ)设关于x的方程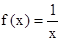 的两实数根为x1、x2.
的两实数根为x1、x2.
试问:是否存在实数m,使得不等式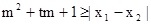 对任意a∈A及t∈[-1,1]恒成立?若存在,求出m的取值范围;若不存在,请说明理由?
对任意a∈A及t∈[-1,1]恒成立?若存在,求出m的取值范围;若不存在,请说明理由?
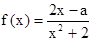 (x∈R)在区间[-1,1]上是增函数
(x∈R)在区间[-1,1]上是增函数(Ⅰ)求实数a的值所组成的集合A
(Ⅱ)设关于x的方程
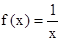 的两实数根为x1、x2.
的两实数根为x1、x2.试问:是否存在实数m,使得不等式
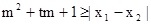 对任意a∈A及t∈[-1,1]恒成立?若存在,求出m的取值范围;若不存在,请说明理由?
对任意a∈A及t∈[-1,1]恒成立?若存在,求出m的取值范围;若不存在,请说明理由? (Ⅰ)
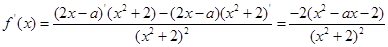 2分
2分因为函数f(x)在区间[-1,1]上是增函数,所以f‘(x)≥0在区间x∈[-1,1]恒成立
即有x2-ax-2≤0在区间[-1,1]上恒成立。 构造函数g(x)=x2-ax-2
∴满足题意的充要条件是:
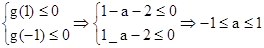
所以所求的集合A[-1,1] (7分)
(Ⅱ)由题意得:
 得到:x2-ax-2=0 (8分)
得到:x2-ax-2=0 (8分)因为△=a2+8>0 所以方程恒有两个不等的根为x1、x2由根与系数的关系有:
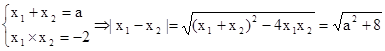 (9分)
(9分)因为a∈A即a∈[-1,1],所以
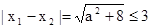 要使不等式
要使不等式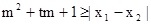 对任意a∈A及t∈[-1,1]恒成立,当且仅当
对任意a∈A及t∈[-1,1]恒成立,当且仅当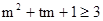 对任意的t∈[-1,1]恒成立 (11分)
对任意的t∈[-1,1]恒成立 (11分)构造函数φ(x)=m2+tm-2=mt+(m2-2) ≥0对任意的t∈[-1,1]恒成立的充要条件是
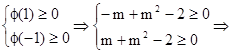 m≥2或m≤-2.故存在实数m满足题意且为
m≥2或m≤-2.故存在实数m满足题意且为{m| m≥2或m≤-2}为所求 (14分)
同答案

练习册系列答案
相关题目
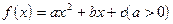 ,方程
,方程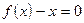 的两个根
的两个根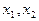 满足
满足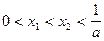 . 当
. 当 时,证明
时,证明 .
.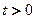 ,关于
,关于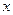 的方程
的方程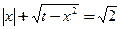 ,则这个方程有相异实根的个数情况是_________________.
,则这个方程有相异实根的个数情况是_________________.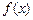 对
对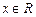 都满足
都满足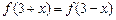 ,且方程
,且方程 恰有6个不同的实数根,则这6个实根的和为()
恰有6个不同的实数根,则这6个实根的和为()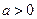 且
且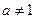 ,求使方程
,求使方程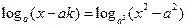 有解时的
有解时的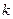 的取值范围。
的取值范围。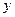 表示成
表示成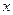 的函数,并写出该函数的定义域.
的函数,并写出该函数的定义域.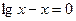 根的个数为( )
根的个数为( )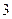
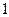
 的图象如下所示, 方程
的图象如下所示, 方程 有且仅有_▲_个根
有且仅有_▲_个根 .
.