题目内容
【题目】已知f（x）=x（ 
+ 
），
（1）试判断f（x）的奇偶性，
（2）求证f（x）＞0．
【答案】
（1）解：由f（x）=x（ 
+ 
）=x 
由2x﹣1≠0，可得x≠0，
则定义域关于原点对称，
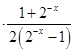f（﹣x）=﹣x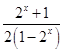 
=﹣x 
=x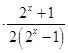 
=f（x），
则f（x）为偶函数
（2）证明：当x＞0时，2x＞1，即2x﹣1＞0，2x+1＞0，
则f（x）=x（ + ）＞0，
由f（x）为偶函数，即有f（﹣x）=f（x），
则x＜0时，f（x）＞0成立．
则对于x≠0的任何实数，都有f（x）＞0
【解析】（1）求出函数的定义域，再计算f（﹣x），与f（x）比较，即可判断函数的奇偶性；（2）运用指数函数的单调性和f（x）的奇偶性即可证得f（x）＞0．
【考点精析】解答此题的关键在于理解函数的值域的相关知识，掌握求函数值域的方法和求函数最值的常用方法基本上是相同的．事实上，如果在函数的值域中存在一个最小（大）数，这个数就是函数的最小（大）值．因此求函数的最值与值域，其实质是相同的，以及对函数的奇偶性的理解，了解偶函数的图象关于y轴对称；奇函数的图象关于原点对称．
练习册系列答案
相关题目
