题目内容
【题目】函数f(x)的定义域为R,并满足以下条件:①对任意x∈R,有f(x)>0;②对任意x,y∈R,有f(xy)=[f(x)]y;③ ![]() .
.
(1)求证:f(x)在R上是单调增函数;
(2)若f(4x+a2x+1﹣a2+2)≥1对任意x∈R恒成立,求实数a的取值范围.
【答案】
(1)证明:令x= ![]() ,y=3得f(1)=[f(
,y=3得f(1)=[f( ![]() )]3,∵
)]3,∵ ![]() .∴所以f(1)>1.
.∴所以f(1)>1.
令x=1,则f(xy)=f(y)=[f(1)]y,
即f(x)=[f(1)]x,为底数大于1的指数函数,
所以函数f(x)在R上单调递增
(2)解:f(xy)=[f(x)]y中令x=0,y=2有f(0)=[f(0)]2,对任意x∈R,有f(x)>0,
故f(0)=1,
f(4x+a2x+1﹣a2+2)≥1即f(4x+a2x+1﹣a2+2)≥f(0),
由(1)有f(x)在R上是单调增函数,即:4x+a2x+1﹣a2+2≥0任意x∈R恒成立
令2x=t,t>0则t2+2at﹣a2+2≥0在(0,+∞)上恒成立.
i)△≤0即4a2﹣4(2﹣a2)≤0得﹣1≤a≤1;
ii)  得
得 ![]() .
.
综上可知 ![]()
【解析】(1)利用赋值法求f(1),然后根据指数函数的性质确定函数的单调性.(2)利用函数的单调性将不等式转化为4x+a2x+1﹣a2+2≥0任意x∈R恒成立,然后利用指数不等式的性质求a的取值范围.

【题目】4月23人是“世界读书日”,某中学在此期间开展了一系列的读书教育活动,为了解本校学生课外阅读情况,学校随机抽取了100名学生对其课外阅读时间进行调查,下面是根据调查结果绘制的学生日均课外阅读时间(单位:分钟)的频率分布直方图,若将日均课外阅读时间不低于60分钟的学生称为“读书谜”,低于60分钟的学生称为“非读书谜” 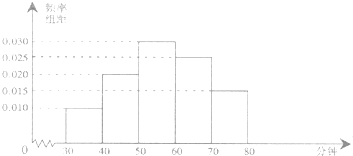
(1)根据已知条件完成下面2×2的列联表,并据此判断是否有99%的把握认为“读书谜”与性别有关?
非读书迷 | 读书迷 | 合计 | |
男 | 15 | ||
女 | 45 | ||
合计 |
(2)将频率视为概率,现在从该校大量学生中,用随机抽样的方法每次抽取1人,共抽取3次,记被抽取的3人中的“读书谜”的人数为X,若每次抽取的结果是相互独立的,求X的分布列,期望E(X)和方程D(X) 附:K2= ![]() n=a+b+c+d
n=a+b+c+d
P(K2≥k0) | 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |