题目内容
如图,在四棱锥 中,底面
中,底面 是正方 形,侧棱
是正方 形,侧棱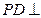 底面
底面 ,
, ,点
,点 是
是 的中点,作
的中点,作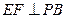 交
交 于点
于点

(1)求证: ∥平面
∥平面
(2)求证: 平面
平面
 中,底面
中,底面 是正方 形,侧棱
是正方 形,侧棱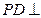 底面
底面 ,
, ,点
,点 是
是 的中点,作
的中点,作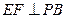 交
交 于点
于点

(1)求证:
 ∥平面
∥平面
(2)求证:
 平面
平面
略
方法一:

(1)
 两两垂直,以O为原点,射线
两两垂直,以O为原点,射线 为非负
为非负 轴,建立空间直角坐标系
轴,建立空间直角坐标系
 ,
, ,
, ,
, ,
, ,
,
 ,
, ,
, 2分
2分
可求得平面 的法向量为
的法向量为
 又
又 平面
平面

 ∥平面
∥平面 4分
4分
(2)

 又
又
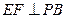


 平面
平面 6分
6分
解:方法二:

(1) 连接BE,BD,AC,设AC交BD于G,
则G为AC的中点
在 中,E为PC的中点,
中,E为PC的中点,
则PA∥EG, 面BED,
面BED, 面BED
面BED
所以 ∥平面
∥平面 3分
3分
(2) PD⊥面ABCD
PD⊥面ABCD
 PD⊥BC
PD⊥BC
 BC⊥CD
BC⊥CD

 BC⊥面PCD
BC⊥面PCD
 面PCD
面PCD
 BC⊥DE
BC⊥DE
 PD=CD,E为PC中点,
PD=CD,E为PC中点, DE⊥PC
DE⊥PC
 DE⊥面PBC
DE⊥面PBC  DE⊥PB,又因为PB⊥EF
DE⊥PB,又因为PB⊥EF

 平面
平面 6分
6分

(1)

 两两垂直,以O为原点,射线
两两垂直,以O为原点,射线 为非负
为非负 轴,建立空间直角坐标系
轴,建立空间直角坐标系 ,
, ,
, ,
, ,
, ,
,  ,
, ,
, 2分
2分可求得平面
 的法向量为
的法向量为
 又
又 平面
平面

 ∥平面
∥平面 4分
4分(2)


 又
又
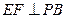


 平面
平面 6分
6分解:方法二:

(1) 连接BE,BD,AC,设AC交BD于G,
则G为AC的中点
在
 中,E为PC的中点,
中,E为PC的中点,则PA∥EG,
 面BED,
面BED, 面BED
面BED所以
 ∥平面
∥平面 3分
3分(2)
 PD⊥面ABCD
PD⊥面ABCD PD⊥BC
PD⊥BC BC⊥CD
BC⊥CD
 BC⊥面PCD
BC⊥面PCD 面PCD
面PCD BC⊥DE
BC⊥DE PD=CD,E为PC中点,
PD=CD,E为PC中点, DE⊥PC
DE⊥PC DE⊥面PBC
DE⊥面PBC  DE⊥PB,又因为PB⊥EF
DE⊥PB,又因为PB⊥EF
 平面
平面 6分
6分
练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目
 的三条侧棱
的三条侧棱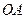 、
、 、
、 两两垂直,且长度均为2.
两两垂直,且长度均为2. 、
、 分别是
分别是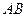 、
、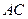 的中点,
的中点, 是
是 的中点,过
的中点,过 、
、 、
、 ,已知
,已知 .
. ⊥面
⊥面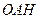 ;
; 的大小.
的大小.
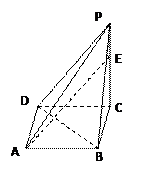 (2)是否不论点E 在何位置都有BD⊥AE,证明你的结论。
(2)是否不论点E 在何位置都有BD⊥AE,证明你的结论。
 ),该几何体的表面积和体积为
),该几何体的表面积和体积为




 cm3
cm3 cm3
cm3 cm3
cm3 cm3
cm3 )为
)为



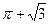




 的面对角线
的面对角线 上存在一点
上存在一点 使得
使得 最短,则
最短,则

 .
.