题目内容
20.在直角坐标系中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,己知曲线C1的方程为ρ=2cosθ+2sinθ,直线C2的参数方程为$\left\{\begin{array}{l}{x=-1+t}\\{y=-1-t}\end{array}\right.$(t为参数)(Ⅰ)将C1的方程化为直角坐标方程;
(Ⅱ)P为C1上一动点,求P到直线C2的距离的最大值和最小值.
分析 (Ⅰ)由ρ=x2+y2、ρcosθ=x、ρsinθ=y,将曲线C1的方程:ρ=2cosθ+2sinθ化为直角坐标方程;
(Ⅱ)将直线C2的参数方程消去t化为直角坐标方程,利用点到直线的距离求出圆心C1(1,1)到直线C2的距离d,判断出直线与圆的位置关系,即可求出答案.
解答 解:(Ⅰ)因为曲线C1的方程为ρ=2cosθ+2sinθ,则ρ2=2ρcosθ+2ρsinθ,
所以C1的直角坐标方程是x2+y2=2x+2y,即(x-1)2+(y-1)2=2;
(Ⅱ)因为直线C2的参数方程为$\left\{\begin{array}{l}{x=-1+t}\\{y=-1-t}\end{array}\right.$(t为参数)
所以直线C2的直角坐标方程为x+y+2=0,
因为圆心C1(1,1)到直线C2的距离d=$\frac{|1+1+2|}{\sqrt{2}}$=2$\sqrt{2}$$>\sqrt{2}$,
则直线与圆相离,
所以求P到直线C2的距离的最大值是3$\sqrt{2}$,最小值$\sqrt{2}$.
点评 本题考查极坐标方程及参数方程化为直角坐标方程,点到直线的距离公式,以及直线与圆的位置关系,属于中档题.

练习册系列答案
相关题目
10.把分别标有“A”“B”“C”的三张卡片随意的排成一排,则能使卡片从左到右可以念成“ABC”和“CBA”的概率是( )
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{4}$ |
8.在对人们的休闲方式的一次调查中,共调查了120人,其中女性65人,男性55人.女性中有40人主要的休闲方式是看电视,另外25人主要的休闲方式是运动;男性中有20人主要的休闲方式是看电视,另外35人主要的休闲方式是运动.${K^2}=\frac{{n{{({ab-bc})}^2}}}{{({a+b})({c+d})({a+c})({b+d})}}$
其中n=a+b+c+d
(1)根据以上数据建立一个2×2的列联表;
(2)能够以多大的把握认为性别与休闲方式有关系,为什么?
其中n=a+b+c+d
| P(K2≥k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(2)能够以多大的把握认为性别与休闲方式有关系,为什么?
15.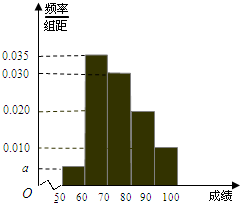 某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:
某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:
(1)求图中a的值;
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均数.
 某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:
某校100名学生期中考试数学成绩的频率分布直方图如图,其中成绩分组区间如下:| 组号 | 第一组 | 第二组 | 第三组 | 第四组 | 第五组 |
| 分组 | [50,60) | [60,70) | [70,80) | [80,90) | [90,100] |
(2)根据频率分布直方图,估计这100名学生期中考试数学成绩的平均数.
5.已知集合A={x|2<x<5},B={x|(x-1)(x-3)<0},则A∩B=( )
| A. | (1,3) | B. | (1,5) | C. | (2,3) | D. | (2,5) |
9.在△ABC中,AB=3,AC=2,$\overrightarrow{AD}$=$\frac{1}{2}$$\overrightarrow{AB}$+$\frac{3}{4}$$\overrightarrow{AC}$,则直线AD通过△ABC的( )
| A. | 垂心 | B. | 外心 | C. | 内心 | D. | 重心 |
10.抛物线的顶点在原点,准线方程为x=3,则抛物线方程为( )
| A. | y2=-12x | B. | y2=-6x | C. | y2=12x | D. | y2=6x |