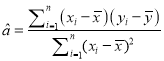题目内容
【题目】若函数y=f(x)的导函数为y=f′(x),且f′(x)=sin2x﹣ ![]() cos2x,则下列说法正确的是( )
cos2x,则下列说法正确的是( )
A.y=f(x)的周期为 ![]()
B.y=f(x)在[0, ![]() ]上是减函数
]上是减函数
C.y=f(x)的图象关于直线x= ![]() 对称
对称
D.y=f(x)是偶函数
【答案】B
【解析】解:∵f′(x)=sin2x﹣ ![]() cos2x,
cos2x,
∴f(x)=﹣ ![]() cos2x﹣
cos2x﹣ ![]() sin2x+c,(c是常数)
sin2x+c,(c是常数)
则f(x)=﹣cos(2x﹣ ![]() )+c,
)+c,
则函数的周期T= ![]() ,故A错误;
,故A错误;
当0≤x≤ ![]() 时,0≤2x≤
时,0≤2x≤ ![]() ,﹣
,﹣ ![]() ≤2x﹣
≤2x﹣ ![]() ≤0,此时y=cos(2x﹣
≤0,此时y=cos(2x﹣ ![]() )为增函数,y=﹣cos(2x﹣
)为增函数,y=﹣cos(2x﹣ ![]() )+c为减函数,故B正确;
)+c为减函数,故B正确;
∵f( ![]() )=﹣cos(2×
)=﹣cos(2× ![]() ﹣
﹣ ![]() )+c=﹣cos
)+c=﹣cos ![]() +c不是最值,
+c不是最值,
∴y=f(x)的图象关于直线x= ![]() 不对称,故C错误;
不对称,故C错误;
∵f(0)=﹣cos(﹣ ![]() )+c不是最值,
)+c不是最值,
∴函数f(x)关于x=0不对称,则函数f(x)不是偶函数,
故D错误.
故选:B.
【考点精析】认真审题,首先需要了解命题的真假判断与应用(两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系),还要掌握基本求导法则(若两个函数可导,则它们和、差、积、商必可导;若两个函数均不可导,则它们的和、差、积、商不一定不可导)的相关知识才是答题的关键.

【题目】某企业为了对新研发的一批产品进行合理定价,将产品按事先拟定的价格进行试销,得到一组销售数据![]() 2,
2,![]() ,如表所示:
,如表所示:
试销单价 | 4 | 5 | 6 | 7 | 8 | 9 |
产品销量 | 90 | 84 | 83 | 80 | q | 68 |
已知![]() .
.
![]() 求表格中q的值;
求表格中q的值;
![]() 已知变量x,y具有线性相关性,试利用最小二乘法原理,求产品销量y关于试销单价x的线性回归方程
已知变量x,y具有线性相关性,试利用最小二乘法原理,求产品销量y关于试销单价x的线性回归方程![]() 参考数据
参考数据![]() ;
;
![]() 用
用![]() 中的回归方程得到的与
中的回归方程得到的与![]() 对应的产品销量的估计值记为
对应的产品销量的估计值记为![]() 2,
2,![]() ,
,![]() 当
当![]() 时,则称
时,则称![]() 为一个“理想数据”
为一个“理想数据”![]() 试确定销售单价分别为4,5,6时有哪些是“理想数据”.
试确定销售单价分别为4,5,6时有哪些是“理想数据”.