题目内容

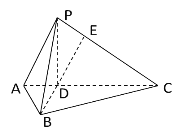
【题目】如图，已知点P是平行四边形ABCD所在平面外一点，M、N分别是AB、PC的中点．

（1）求证：MN∥平面PAD；

（2）在PB上确定一个点Q，使平面MNQ∥平面PAD.

【答案】(1)见解析；(2)见解析.

【解析】

（1）取PD的中点H,易证得AMNH为平行四边形，从而证得MN∥AH，即证得结论；

（2）由平面MNQ∥平面PAD,则应有MQ∥PA，利用中位线定理可确定位置.

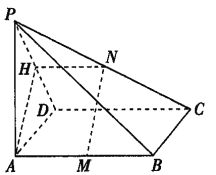
(1)如图,取PD的中点H,

连接AH、NH.由N是PC的中点,H是PD的中点,知NH∥DC,NH=DC.

由M是AB的中点,知AM∥DC,AM=DC

.

∴NH∥AM,NH=AM,所以AMNH为平行四边形.

∴MN∥AH.

由MN平面PAD,AH平面PAD,

知MN∥平面PAD.

(2)若平面MNQ∥平面PAD,则应有MQ∥PA,

∵M是AB中点,∴Q是PB的中点.

即当Q为PB的中点时,平面MNQ∥平面PAD.

练习册系列答案
相关题目

【题目】若函数y=f（x）的导函数为y=f′（x），且f′（x）=sin2x﹣ cos2x，则下列说法正确的是（ ）
A.y=f（x）的周期为
B.y=f（x）在[0， ]上是减函数
C.y=f（x）的图象关于直线x= 对称
D.y=f（x）是偶函数

【题目】已知正三角形ABC边长为2，将它沿高AD翻折，使点B与点C间的距离为 ，此时四面体ABCD的外接球的表面积为 ．

【题目】已知函数f（x）=lnx。

（1）求曲线y=f（x）在点（1，f（1））处的切线方程；

（2）求证：当x>0时，f（x）≥l-；

（3）若x-1>alnx对任意x>1恒成立，求实数a的最大值。

【题目】a、b、c为三条不重合的直线，α、β、γ为三个不重合的平面，现给出六个命题．

①a∥b； ②a∥b； ③α∥β；

④α∥β； ⑤a∥α； ⑥a∥α，

其中正确的命题是________．(填序号)

【题目】已知函数.

（1）判断并证明函数的奇偶性；

（2）判断当时函数的单调性，并用定义证明；

（3）若定义域为，解不等式.

【答案】（1）奇函数（2）增函数（3）

【解析】试题分析：（1）判断与证明函数的奇偶性，首先要确定函数的定义域是否关于原点对称，再判断f(-x)与f(x)的关系，如果对定义域上的任意x，都满足f(-x)=f(x)就是偶函数，如果f(-x)=-f(x)就是奇函数，否则是非奇非偶函数。（2）利函数单调性定义证明单调性，按假设，作差，化简，判断，下结论五个步骤。（3）由（1）（2）奇函数在（-1，1）为单调函数，

原不等式变形为f(2x-1)<-f(x),即f(2x-1)<f(-x),再由函数的单调性及定义（-1，1）求解得x范围。

试题解析：（1）函数为奇函数．证明如下：

定义域为

又

为奇函数

（2）函数在（-1，1）为单调函数．证明如下：

任取，则

，

即

故在（-1，1）上为增函数

（3）由（1）、（2）可得

则

解得：

所以，原不等式的解集为

【点睛】

（1）奇偶性：判断与证明函数的奇偶性，首先要确定函数的定义域是否关于原点对称，再判断f(-x)与f(x)的关系，如果对定义域上的任意x，都满足f(-x)=f(x)就是偶函数，如果f(-x)=-f(x)就是奇函数，否则是非奇非偶函数。

（2）单调性：利函数单调性定义证明单调性，按假设，作差，化简，定号，下结论五个步骤。

【题型】解答题
【结束】
22

【题目】已知函数.

（1）若的定义域和值域均是，求实数的值；

（2）若在区间上是减函数，且对任意的，都有，求实数的取值范围；

（3）若，且对任意的，都存在，使得成立，求实数的取值范围.

【题目】设常数使方程在区间上恰有三个解且，则实数的值为（　　）

A. B. C. D.

【题目】如图，在三棱锥中，，，，且，，，，为上一点，.

（1）求证：平面；

（2）求异面直线和所成角的余弦值.

【题目】如图，在三棱锥中，SA=SB=AB=BC=CA=6，且侧面ASB⊥底面ABC，则三棱锥S－ABC外接球的表面积为（ ）

A. 60π B. 56π C. 52π D. 48π

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网