Question

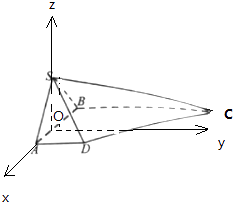
【题目】如图，在四棱锥S﹣ABCD中，底面ABCD是直角梯形，AB垂直于AD和BC，平面SAB⊥底面ABCD，且SA=SB= ，AD=1，AB=2，BC=3．

（1）求证：SB⊥平面SAD；
（2）求二面角D﹣SC﹣B的余弦值．

Answer 1

【答案】
（1）证明：∵平面SAB⊥底面ABCD，面SAB∩平面ABCD=AB，

DA⊥AB，DA面ABCD，

∴DA⊥平面SAB，SB平面SAB，∴SB⊥AD，

又SA=SB= ，AB=2，∴SA⊥SB，SA∩AD=A，

∴SB⊥平面SAD．

（2）解：过点S作SO⊥AB于O，则SO⊥底面ABCD，

过O作OE∥AD，

以O为原点，OA，OE，OS所在直线为x，y，z轴，建立空间直角坐标系，

则A（1，0，0），B（﹣1，0，0），C（﹣1，3，0），D（1，1，0），S（0，0，1），

∴ =（1，1，﹣1）， =（﹣2，2，0），

设平面SCD的一个法向量 =（x，y，z），

则 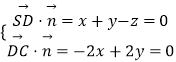，取x=1，得 =（1，1，2），

设平面SBC的一个法向量为 =（a，b，c），

=（﹣1，0，﹣1）， =（0，3，0），

则 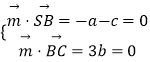，取a=1，得 =（1，0，﹣1），

cos＜ ＞= = =﹣ ，

由图形得二面角D﹣SC﹣B的平面角是钝角，

∴二面角D﹣SC﹣B的余弦值为﹣ ．

【解析】（1）推导出SB⊥AD，SA⊥SB，由此能证明SB⊥平面SAD．（2）以O为原点，OA，OE，OS所在直线为x，y，z轴，建立空间直角坐标系，利用向量法能求出二面角D﹣SC﹣B的余弦值．
【考点精析】认真审题，首先需要了解直线与平面垂直的判定(一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想)．