题目内容
13.给出下列四个命题:①已知命题p:?x∈R,tanx=2;命题q:?x∈R,x2-x+1≥0,则命题“p∧q”为真命题;
②函数f(x)=2x+2x-3在定义域内有且只有一个零点;
③已知圆O:x2+y2=5,直线l:xcosθ+ysinθ=1(0<θ<$\frac{π}{2}})$).则圆O上到直线l的距离等于1的点的个数为2;
④用数学归纳法证明(n+1)(n+2)…(n+n)=2n•1•3…(2n-1)(n∈N*)的过程中,由n=k到n=k+1时,左边需增添的一个因式是2(2k+1).其中,真命题的序号是①②④(把你认为正确的命题序号都填上).
分析 ①根据命题p、q的真假来断定p∧q的真假.②根据两个函数的增减性来断定函数的零点个数.③有直线到圆的距离得出圆上o到直线的距离等于1的个数.根据“k”到“k+1”时,等式左边添加两项2k+1,2k+2,同时减少一项k+1,可判断④的真假
解答 解:命题p:?x∈R,tanx=2是真命题.x2-x+1=(x-$\frac{1}{2}$)2+$\frac{3}{4}$≥0恒成立.所以命题“p∧q”为真命题.①对.
f(x)=2x+2x-3.可得y=2x为增函数.y=3-2x为减函数.所以函数f(x)=2x+2x-3在定义域内有且只有一个零点,②对.
圆心(0,0)到直线xcosθ+ysinθ=1(0<θ<$\frac{π}{2}})$)的距离为1.圆的半径为$\sqrt{5}$
则圆O上到直线l的距离等于1的点的个数为4;③错.
由数学归纳法证明(n+1)(n+2)…(n+n)=2n•1•3…(2n-1)(n∈N*)时,从“k”到“k+1”的证明,左边需增添的一个因式是$\frac{(2k+1)(2k+2)}{k+1}$=2(2k+1),故④正确.所以选①②④
点评 本题考查的知识点是命题的真假判断与应用,数学归纳法的证明步骤,函数零点的个数判断等基础知识点是解答本题的关键

练习册系列答案
相关题目
1.设集合U=R,A={x|y=ln(1-x)},B={x|x2-3x≥0},则A∩∁UB=( )
| A. | {x|0<x<1} | B. | {x|1<x<3} | C. | {x|0<x<3} | D. | {x|x<1} |
18.已知f(x)是定义在R上的周期为2的奇函数,当x∈(0,1)时,f(x)=3x-1,则f($\frac{2015}{2}$)=( )
| A. | $\sqrt{3}$+1 | B. | -$\sqrt{3}$+1 | C. | $\sqrt{3}$-1 | D. | -$\sqrt{3}$-1 |
5.某医疗研究所为了检验某种血清能起到预防感冒的作用,把500名使用血清的人与另外500名未用血清的人一年中的感冒记录作比较,利用2×2列联表计算得k2≈3.918.
附表:
则作出“这种血清能起到预防感冒的作用”出错的可能性不超过( )
附表:
| P(k2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
| A. | 95% | B. | 5% | C. | 97.5% | D. | 2.5% |
3.已知点A=(-1,1)、B=(1,2)、C=(-3,2),则向量$\overrightarrow{AB}$在$\overrightarrow{AC}$方向上的投影为( )
| A. | -$\frac{3}{5}$ | B. | $\frac{3\sqrt{5}}{5}$ | C. | -$\frac{3\sqrt{5}}{5}$ | D. | $\frac{3}{5}$ |
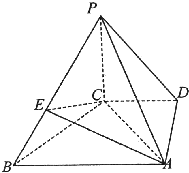 如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,PE=2BE.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD,底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2AD=2CD=2,PE=2BE.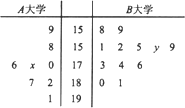 济南天下第一泉风景区为了做好宣传工作,准备在A和B两所大学分别招募8名和12名志愿者,将这20名志愿者的身高编成如右茎叶图(单位:cm).若身高在175cm以上(包括175cm)定义为“高精灵”,身高在175cm以下 (不包括175cm)定义为“帅精灵”.已知A大学志愿者的身高的平均数为176cm,B大学志愿者的身高的中位数为168cm.
济南天下第一泉风景区为了做好宣传工作,准备在A和B两所大学分别招募8名和12名志愿者,将这20名志愿者的身高编成如右茎叶图(单位:cm).若身高在175cm以上(包括175cm)定义为“高精灵”,身高在175cm以下 (不包括175cm)定义为“帅精灵”.已知A大学志愿者的身高的平均数为176cm,B大学志愿者的身高的中位数为168cm.