题目内容
【题目】如图，点
是双曲线
上的动点，
是双曲线的焦点，M是
的平分线上一点，且
，某同学用以下方法研究
：延长
交
于点N，可知
为等腰三角形，且M为
的中点，得
，类似地：点是椭圆
上的动点，椭圆的焦点，M是的平分线上一点，且则的取值范围是______
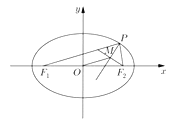
【答案】
【解析】
利用M是∠F1PF2平分线上的一点，且F2M⊥MP，判断OM是三角形F1F2N的中位线，把OM用PF1，PF2表示，再利用椭圆的焦半径公式，转化为用椭圆上点的横坐标表示，借助椭圆的范围即可求出OM的范围．
如图，延长F2M，交PF1与N点，
∵PM是∠F1PF2平分线，且
0，
且F2M⊥MP，
∴|PN|＝|PF2|，M为F2N的中点，
连接OM，
∵O为F1F2中点，M为F2N中点，
∴|OM|
|F1N|||PF1|﹣|PN||||PF1|﹣|PF2||
∵在椭圆
1（a＞b＞0）中，
设P点坐标为（x0，y0）
则|PF1|＝a+ex0，|PF2|＝a﹣ex0，
∴||PF1|﹣|PF2||＝|a+ex0﹣a+ex0|＝|2ex0|＝2e|x0|
|x0|，
即有|OM|
|x0|，
∵P点在椭圆1（a＞b＞0）上，
∴|x0|∈（0，a]，
又∵当|x0|＝a时，F2M⊥MP不成立，∴|x0|∈（0，a），
∴|OM|∈（0，c）=．
故答案为：．
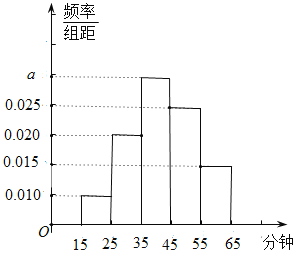
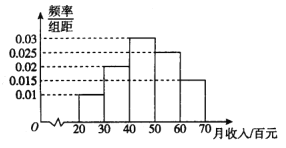
【题目】为了调查煤矿公司员工的饮食习惯与月收入之间的关系，随机抽取了30名员工，并制作了这30人的月平均收入的频率分布直方图和饮食指数表（说明：图中饮食指数低于70的人，饮食以蔬菜为主；饮食指数高于70的人，饮食以肉类为主）．其中月收入4000元以上员工中有11人饮食指数高于70.
20 | 21 | 21 | 25 | 32 | 33 |
36 | 37 | 42 | 43 | 44 | 45 |
45 | 58 | 58 | 59 | 61 | 66 |
74 | 75 | 76 | 77 | 77 | 78 |
78 | 82 | 83 | 85 | 86 | 90 |
（Ⅰ）是否有95%的把握认为饮食习惯与月收入有关系？若有请说明理由，若没有，说明理由并分析原因；
（Ⅱ）以样本中的频率作为概率，从该公司所有主食蔬菜的员工中随机抽取3人，这3人中月收入4000元以上的人数为
，求的分布列与期望；
（Ⅲ）经调查该煤矿公司若干户家庭的年收入
（万元）和年饮食支出
（万元）具有线性相关关系，并得到关于的回归直线方程：
.若该公司一个员工与其妻子的月收入恰好都为这30人的月平均收入（该家庭只有两人收入），估计该家庭的年饮食支出费用.
附：
.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【题目】某学生对其亲属30人的饮食习惯进行了一次调查，并用下图所示的茎叶图表示30人的饮食指数．(说明：图中饮食指数低于70的人，饮食以蔬菜为主；饮食指数高于70的人，饮食以肉类为主)
(1)根据以上数据完成下面的2×2列联表：
主食 蔬菜 | 主食 肉类 | 总计 | |
50岁以下 | |||
50岁以上 | |||
总计 |
(2)能否在犯错误的概率不超过0.010的前提下认为“其亲属的饮食习惯与年龄有关”？并写出简要分析．
附参考公式：
|
|
|
|
|
|
|
|
|
|
|
|
