[题目]如图.在四棱锥P-ABCD中.底面ABCD是平行四边形.且AB＝1.BC＝2. ∠ABC=60°.PA⊥平面ABCD.AE⊥PC于E.下列四个结论:①AB⊥AC,②AB⊥平面PAC,③PC⊥平面ABE,④BE⊥PC．正确的个数是( )A.1B.2C.3D.4 题目和参考答案——青夏教育精英家教网—

题目内容

【题目】如图，在四棱锥P-ABCD中，底面ABCD是平行四边形，且AB＝1，BC＝2， ∠ABC=60°，PA⊥平面ABCD，AE⊥PC于E，

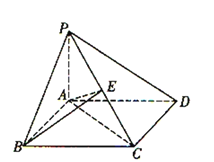
下列四个结论：①AB⊥AC；②AB⊥平面PAC；③PC⊥平面ABE；④BE⊥PC．正确的个数是( )

A.1B.2C.3D.4

【答案】D

【解析】

在中，由余弦定理可求出，再由PA⊥平面ABCD，可证出AB⊥平面PAC，再由AE⊥PC于E，线面垂直的判定定理，可证明PC⊥平面ABE，根据线面垂直的判定,可证出BE⊥PC，因此可知正确命题的个数.

已知由余弦定理可得，所以，即①正确；

由平面ABCD，得，所以平面，②正确；

平面，得，又，所以平面ABE，③正确；

由平面ABE，得，④正确，

故选：D．

练习册系列答案

相关题目

【题目】直线l：ax+ y﹣1=0与x，y轴的交点分别为A，B，直线l与圆O：x2+y2=1的交点为C，D，给出下面三个结论：①a≥1，S△AOB=；②a≥1，|AB|＜|CD|；③a≥1，S△COD＜.其中，所有正确结论的序号是（　　）

A.①②B.②③C.①③D.①②③

【题目】已知数列，记集合.

（1）对于数列，写出集合；

（2）若，是否存在，使得？若存在，求出一组符合条件的；若不存在，说明理由.

（3）若，把集合中的元素从小到大排列，得到的新数列为，若，求的最大值.

【题目】已知对于任意，函数与的图像在上都有三个不同交点.

（1）写出的解析式，并求函数的最大值及此时的x的取值；

（2）若函数在和上单调递增，在上单调递减，且，求的所有可能值.

【题目】环保部门要对所有的新车模型进行广泛测试，以确定它的行车里程的等级，下表是对100辆新车模型在一个耗油单位内行车里程（单位：公里）的测试结果．

分组	频数
	6
	10
	20
	30
	18
	12
	4

（1）做出上述测试结果的频率分布直方图，并指出其中位数落在哪一组；

（2）用分层抽样的方法从行车里程在区间与的新车模型中任取5辆，并从这5辆中随机抽取2辆，求其中恰有一个新车模型行车里程在内的概率．

【题目】“辛卜生公式”给出了求几何体体积的一种计算方法:夹在两个平行平面之间的几何体,如果被平行于这两个平面的任何平面所截,截得的截面面积是截面高（不超过三次）的多项式函数,那么这个几何体的体积,就等于其上底面积、下底面积与四倍中截面面积的和乘以高的六分之一.即:,式中,,,依次为几何体的高,下底面积,上底面积,中截面面积.如图,现将曲线与直线及轴围成的封闭图形绕轴旋转一周得到一个几何体.利用辛卜生公式可求得该几何体的体积( )