题目内容
【题目】为发挥体育核心素养的独特育人价值,越来越多的中学将某些体育项目纳入到学生的必修课程.惠州市某中学计划在高一年级开设游泳课程,为了解学生对游泳的兴趣,某数学研究学习小组随机从该校高一年级学生中抽取了100人进行调查.
(1)已知在被抽取的学生中高一![]() 班学生有6名,其中3名对游泳感兴趣,现在从这6名学生中随机抽取3人,求至少有2人对游泳感兴趣的概率;
班学生有6名,其中3名对游泳感兴趣,现在从这6名学生中随机抽取3人,求至少有2人对游泳感兴趣的概率;
(2)该研究性学习小组在调查中发现,对游泳感兴趣的学生中有部分曾在市级或市级以上游泳比赛中获奖,具体获奖人数如下表所示.若从高一![]() 班和高一
班和高一![]() 班获奖学生中随机各抽取2人进行跟踪调查,记选中的4人中市级以上游泳比赛获奖的人数为
班获奖学生中随机各抽取2人进行跟踪调查,记选中的4人中市级以上游泳比赛获奖的人数为![]() ,求随机变量
,求随机变量![]() 的分布列及数学期望.
的分布列及数学期望.
班级 | 一 | 一 | 一 | 一 | 一 | 一 | 一 | 一 | 一 | 一 |
|
市级 比赛获奖人数 | 2 | 2 | 3 | 3 | 4 | 4 | 3 | 3 | 4 | 2 |
|
市级以上 比赛获奖人数 | 2 | 2 | 1 | 0 | 2 | 3 | 3 | 2 | 1 | 2 |
|
【答案】(1)![]() ;(2)分布列见解析,
;(2)分布列见解析,![]()
【解析】
(1)利用组合数结合古典概型求出从这6名学生中随机抽取3人,至少有2人对游泳有兴趣的概率.
(2)由题意可知ξ的所有可能取值为0,1,2,3,分别求出相应的概率,由此能求出ξ的分布列和E(ξ).
(1)
记事件![]() 从6名学生抽取的3人中恰好有i人有兴趣,
从6名学生抽取的3人中恰好有i人有兴趣,![]() ,1,2,
,1,2,![]() ;
;
则![]() 与
与![]() 互斥
互斥
故所求概率为![]()
![]()
![]() ;
;
(2)由题意知,随机变量![]() 的所有可能取值有0,1,2,3;
的所有可能取值有0,1,2,3;
![]()
![]()
![]()
![]()
则![]() 的分布列为:
的分布列为:
| 0 | 1 | 2 | 3 | |
p |
|
|
|
| … |
数学期望为![]()

 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案【题目】党中央、国务院历来高度重视青少年的健康成长.“少年强则国强”,青少年身心健康、体魄强健、意志坚强、充满活力,是一个民族旺盛生命力的体现,是社会文明进步的标志,是国家综合实力的重要方面.全面实施《国家学生体质健康标准》,把健康素质作为评价学生全面健康发展的重要指标,是新时代的要求.《国家学生体质健康标准》有一项指标是学生体质指数(![]() ),其计算公式为:
),其计算公式为: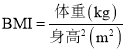 ,当
,当![]() 时,认为“超重”,应加强锻炼以改善
时,认为“超重”,应加强锻炼以改善![]() .某高中高一、高二年级学生共2000人,人数分布如表(a).为了解这2000名学生的
.某高中高一、高二年级学生共2000人,人数分布如表(a).为了解这2000名学生的![]() 指数情况,从中随机抽取容量为160的一个样本.
指数情况,从中随机抽取容量为160的一个样本.
表(a)
性别 年级 | 男生 | 女生 | 合计 |
高一年级 | 550 | 650 | 1200 |
高二年级 | 425 | 375 | 800 |
合计 | 975 | 1025 | 2000 |
(1)为了使抽取的160个学生更具代表性,宜采取分层抽样,试给出一个合理的分层抽样方案,并确定每层应抽取出的学生人数;
(2)分析这160个学生的![]() 值,统计出“超重”的学生人数分布如表(b).
值,统计出“超重”的学生人数分布如表(b).
表(b)
性别 年级 | 男生 | 女生 |
高一年级 | 4 | 6 |
高二年级 | 2 | 4 |
(ⅰ)试估计这2000名学生中“超重”的学生数;
(ⅱ)对于该校的2000名学生,应用独立性检验的知识,可分析出性别变量与年级变量哪一个与“是否超重”的关联性更强.应用卡方检验,可依次得到![]() 的观测值
的观测值![]() ,
,![]() ,试判断
,试判断![]() 与
与![]() 的大小关系.(只需写出结论)
的大小关系.(只需写出结论)