题目内容
已知命题p：“?a＞0，有ea≥1成立”，则￢p为（ ）
| A、?a≤0，有ea≤1成立 | B、?a≤0，有ea≥1成立 | C、?a＞0，有ea＜1成立 | D、?a＞0，有ea≤1成立 |
考点：命题的否定
专题：简易逻辑
分析：根据全称命题的否定是特称命题即可得到结论．
解答：解：全称命题的否定是特称命题，则￢p：?a＞0，有ea＜1成立，
故选：C．
故选：C．
点评：本题主要考查含有量词的命题的否定，比较基础．
练习册系列答案
长江作业本同步练习册系列答案
相关题目
《张邱建算经》有一道题：今有女子不善织布，逐日所织的布同数递减，初日织五尺，末一日织一尺，计织三十日，问共织布（ ）
| A、110尺 | B、90尺 | C、60尺 | D、30尺 |
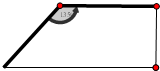两直立矮墙成135°二面角，现利用这两面矮墙和篱笆围成一个面积为54m2的直角梯形菜园（墙足够长），则所用篱笆总长度的最小值为（ ）| A、16m | ||
| B、18m | ||
| C、22.5m | ||
D、15
|
已知命题p：a=1是?x＞0，x+
≥2的充要条件：命题q：?x∈R，x2-x+1＜0．则下列结论中正确的是（ ）
| a |
| x |
| A、p∧q为真命题 |
| B、p∧￢q为真命题 |
| C、￢p∧q为真命题 |
| D、￢p∧￢q为真命题 |
定义“正对数”：ln+x=
，现有四个命题：
①若a＞0，b＞0，则ln+（ab）=bln+a
②若a＞0，b＞0，则ln+（ab）=ln+a+ln+b
③若a＞0，b＞0，则ln+(
)≥ln+a-ln+b
④若a＞0，b＞0，则ln+（a+b）≤ln+a+ln+b+ln2
其中正确的命题有（ ）
|
①若a＞0，b＞0，则ln+（ab）=bln+a
②若a＞0，b＞0，则ln+（ab）=ln+a+ln+b
③若a＞0，b＞0，则ln+(
| a |
| b |
④若a＞0，b＞0，则ln+（a+b）≤ln+a+ln+b+ln2
其中正确的命题有（ ）
| A、①③④ | B、①②③ |
| C、①②④ | D、②③④ |
若p：φ=
+kπ，k∈Z，q：f（x）=sin（ωx+φ）（ω≠0）是偶函数，则p是q的（ ）
| π |
| 2 |
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |