题目内容

【题目】已知圆x2+y2=8内有一点P0（-1，2），AB为过点P0且倾斜角为α的弦.

（1）当α=时，求AB的长；

（2）当弦AB被点P0平分时，写出直线AB的方程(用直线方程的一般式表示)．

【答案】（1）；（2）x－2y＋5＝0

【解析】

(1)先求出直线的方程,再利用垂径定理求解即可.

(2) 当弦AB被点P0平分时利用得出的斜率,再用点斜式求解化简成一般方程即可.

（1）过点O做OG⊥AB于G,连结OA,当α=135°时,直线AB的斜率为-1,

故直线AB的方程x+y-1=0, ∴OG=,

∵, ∴

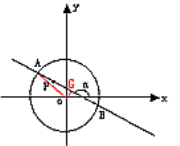
（2）当弦AB被点P0平分时,OP0⊥AB, 直线OP0的斜率为－2,所以直线AB的斜率为．根据直线的点斜式方程,直线AB的方程为,即x－2y＋5＝0．

练习册系列答案
相关题目

【题目】已知服从正态分布的随机变量在区间，，内取值的概率分别为0.6826，0.9544，0.9974.若某种袋装大米的质量（单位：）服从正态分布，任意选一袋这种大米，质量在的概率为_．

【题目】已知椭圆C： （a>b>0），四点P1（1,1），P2（0,1），P3（–1， ），P4（1， ）中恰有三点在椭圆C上.

（1）求C的方程；

（2）设直线l不经过P2点且与C相交于A，B两点.若直线P2A与直线P2B的斜率的和为–1，证明：l过定点.

【题目】如图，已知椭圆的左、右焦点分别为、，点为椭圆上任意一点，关于原点的对称点为，有，且的最大值.

（1）求椭圆的标准方程；

（2）若是关于轴的对称点，设点，连接与椭圆相交于点，问直线与轴是否交于一定点.如果是，求出该定点坐标；如果不是，说明理由.

【题目】选修4-4：坐标系与参数方程

在平面直角坐标系中，曲线的参数方程为（为参数），将曲线上所有点的横坐标缩短为原来的，纵坐标缩短为原来的，得到曲线，在以坐标原点为极点，轴的正半轴为极轴的极坐标系中，直线的极坐标方程为.

（1）求曲线的极坐标方程及直线的直角坐标方程；

（2）设点为曲线上的任意一点，求点到直线的距离的最大值.

【题目】已知函数．

(1)讨论的单调性；

(2)当时，，求的最大整数值．

【题目】已知函数f（x）＝ex（x﹣a）2+4．

（1）若f（x）在（﹣∞，+∞）上单调递增，求a的取值范围；

（2）若x≥0，不等式f（x）≥0恒成立，求a的取值范围．

【题目】如图，在三棱柱中，平面，为边上一点，，.

（1）证明：平面平面.

（2）若，试问：是否与平面平行？若平行，求三棱锥的体积；若不平行，请说明理由.

【题目】某市准备引进优秀企业进行城市建设. 城市的甲地、乙地分别对5个企业（共10个企业）进行综合评估，得分情况如茎叶图所示.

（Ⅰ）根据茎叶图，求乙地对企业评估得分的平均值和方差；

（Ⅱ）规定得分在85分以上为优秀企业. 若从甲、乙两地准备引进的优秀企业中各随机选取1个，求这两个企业得分的差的绝对值不超过5分的概率.

注：方差

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网