Question

【题目】函数的图象与x轴交于点A，B(点A在点B的左侧)，函数的图象与x轴交于点C，D(点C在点D的左侧)，其中，.

(1)求证:函数与的图象交点落在一条定直线上;

(2)若，求a，b和k应满足的关系式:

(3)是否存在函数和，使得B，C为线段AD的三等分点?若存在，求的值，若不存在，说明理由.

Answer 1

【答案】(1)见解析;(2);(3)存在，或

【解析】

（1）令，解方程即可求得.

（2）若，可得，ABCD为抛物线与x轴的交点，求出的值，代入上式即可求解.

（3）分类讨论，由BC为线段AD的三等分点，当点B在点C左侧时，，则有，将代入即可；当点C在点B左侧时，，则有，将代入即可求解.

(1)当时，，

∵，

∴，

∴函数与的图象交点落在一条定直线上;

(2)若，则，ABCD为抛物线与x轴的交点，可得

，，

，，

代入得

，

所以;

(3)因为BC为线段AD的三等分点，

当点B在点C左侧时，，则有，

∴，

∴，

整理得:，

∴，

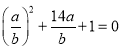解得或;

当点C在点B左侧时，，则有，

∴，

∴，

即，

整理得:，

∵，

∴，

即，

，

∴，

，方程无解，

综上，的值为或.