题目内容
3.已知P是△ABC内一点,$\overrightarrow{PB}$+$\overrightarrow{PC}$+2$\overrightarrow{PA}$=0,现将一粒黄豆随机投入△ABC内,则该粒黄豆落在△PAC内的概率是( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{4}$ | D. | $\frac{1}{5}$ |
分析 本题符合几何概型的意义,只要画出满足条件的图形,数形结合找出满足条件的△APC的面积大小与△ABC面积的大小之间的关系,再根据几何概型的计算公式进行求解.
解答 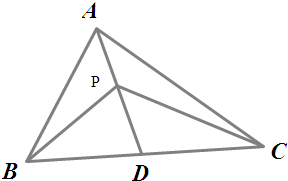 解:如图示,取BC的中点为D,连接PA,PB,PC,
解:如图示,取BC的中点为D,连接PA,PB,PC,
则2$\overrightarrow{PD}=\overrightarrow{PB}+\overrightarrow{PC}$,又P点满足$\overrightarrow{PB}$+$\overrightarrow{PC}$+2$\overrightarrow{PA}$=0,
故有$\overrightarrow{PD}+\overrightarrow{PA}=\overrightarrow{0}$,可得三点A,P,D共线且$\overrightarrow{AP}=\frac{1}{2}\overrightarrow{AD}$,
即P点为A,D的中点时满足$\overrightarrow{PB}$+$\overrightarrow{PC}$+2$\overrightarrow{PA}$=0,
此时S△APC=$\frac{1}{4}$S△ABC,
故黄豆落在△APC内的概率为$\frac{1}{4}$,
故选:C.
点评 本题考查了几何概型的概率求法;关键是选择公式中的“几何度量”,可以为线段长度、面积、体积等,而且这个“几何度量”只与“大小”有关,而与形状和位置无关.解决的步骤均为:求出满足条件A的基本事件对应的“几何度量”N(A),再求出总的基本事件对应的“几何度量”N,最后根据公式解答.

练习册系列答案
相关题目
14.已知平面向量$\overrightarrow{α}$,$\overrightarrow{β}$满足|2$\overrightarrow{β}$-$\overrightarrow{α}$|=$\sqrt{3}$,且$\overrightarrow{α}$+$\overrightarrow{β}$与$\overrightarrow{α}$-2$\overrightarrow{β}$的夹角为150°,则|t($\overrightarrow{α}$+$\overrightarrow{β}$)-$\frac{3}{2}$$\overrightarrow{β}$|,(t∈R)的最小值是( )
| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
11.铁矿石A和B的含铁率a,冶炼每万吨铁矿石的CO2的排放量b及每万吨铁矿石的价格c如下表:
某冶炼厂至少要生产1.9(万吨)铁,若要求CO2的排放量不超过2(万吨),求购买铁矿石的最少费用.
| a | b(万吨) | c(百万元) | |
| A | 50% | 1 | 3 |
| B | 70% | 0.5 | 6 |
18.过点(0,5)且在两坐标轴上截距之和为2的直线方程为( )
| A. | 3x+5y+15=0 | B. | 5x+3y-15=0 | C. | 5x-3y+15=0 | D. | 3x-5y-15=0 |
12.使cosx=1-m有意义的m的取值范围为( )
| A. | m≥0 | B. | 0≤m≤2 | C. | -1<m<1 | D. | m<-1或m>1 |