题目内容
4.已知函数f(x)=lnx+ax2+(2-2a)x+$\frac{1}{4a}$(a>0),若存在三个不相等的正实数x1,x2,x3,使得$\frac{{f({x_1})}}{x_1}=\frac{{f({x_2})}}{x_2}=\frac{{f({x_3})}}{x_3}$=3成立,则a的取值范围是($\frac{1}{2e}$,$\frac{\sqrt{2}-1}{2}$).分析 若存在三个不相等的正实数x1,x2,x3,使得$\frac{{f({x_1})}}{x_1}=\frac{{f({x_2})}}{x_2}=\frac{{f({x_3})}}{x_3}$=3成立,等价为方程f(x)=3x存在三个不相等的实根,构造函数,求函数的导数,研究函数的极值,利用极大值大于0,极小值小于0,即可得到结论.
解答 解:若存在三个不相等的正实数x1,x2,x3,使得$\frac{{f({x_1})}}{x_1}=\frac{{f({x_2})}}{x_2}=\frac{{f({x_3})}}{x_3}$=3成立,
即方程f(x)=3x存在三个不相等的实根,
即lnx+ax2+(2-2a)x+$\frac{1}{4a}$=3x,lnx+ax2-(1+2a)x+$\frac{1}{4a}$=0有三个不相等的实根,
设g(x)=lnx+ax2-(1+2a)x+$\frac{1}{4a}$,
则函数的导数g′(x)=$\frac{1}{x}$+2ax-(1+2a)=$\frac{2a{x}^{2}-(1+2a)x+1}{x}$=$\frac{(2ax-1)(x-1)}{x}$,
由g′(x)=0得x=1,x=$\frac{1}{2a}$,
则g(1)=a-1-2a+$\frac{1}{4a}$=-1-a+$\frac{1}{4a}$,
g($\frac{1}{2a}$)=ln$\frac{1}{2a}$+a($\frac{1}{2a}$)2-(1+2a)$\frac{1}{2a}$+$\frac{1}{4a}$=-1-ln2a.
若$\frac{1}{2a}$=1,即a=$\frac{1}{2}$时,g′(x)=$\frac{(x-1)^{2}}{x}$≥0,此时函数g(x)为增函数,不可能有3个根,
若$\frac{1}{2a}$>1,即0<a<$\frac{1}{2}$时,由g′(x)>0得x>$\frac{1}{2a}$或0<x<1,此时函数递增,
由g′(x)<0得1<x<$\frac{1}{2a}$,此时函数递减,
则当x=1时函数g(x)取得极大值g(1)=-1-a+$\frac{1}{4a}$,
当x=$\frac{1}{2a}$时函数g(x)取得极小值g($\frac{1}{2a}$)=-1-ln2a,
此时满足g(1)=-1-a+$\frac{1}{4a}$>0且g($\frac{1}{2a}$)=-1-ln2a<0,
即$\left\{\begin{array}{l}{\frac{-(4{a}^{2}+4a-1)}{4a}>0}\\{ln2a>-1}\end{array}\right.$,即$\left\{\begin{array}{l}{4{a}^{2}+4a-1<0}\\{2a>\frac{1}{e}}\end{array}\right.$,
则$\left\{\begin{array}{l}{\frac{-1-\sqrt{2}}{2}<a<\frac{-1+\sqrt{2}}{2}}\\{a>\frac{1}{2e}}\end{array}\right.$,解得$\frac{1}{2e}$<a<$\frac{\sqrt{2}-1}{2}$.
同理若$\frac{1}{2a}$<1,即a>$\frac{1}{2}$时,由g′(x)>0得x>1或0<x<$\frac{1}{2a}$,此时函数递增,
由g′(x)<0得$\frac{1}{2a}$<x<1,此时函数递减,
则当x=1时函数g(x)取得极小值g(1)=-1-a+$\frac{1}{4a}$,
当x=$\frac{1}{2a}$时函数g(x)取得极大值g($\frac{1}{2a}$)=-1-ln2a,
此时满足g(1)=-1-a+$\frac{1}{4a}$<0且g($\frac{1}{2a}$)=-1-ln2a>0,
即$\left\{\begin{array}{l}{\frac{-(4{a}^{2}+4a-1)}{4a}<0}\\{ln2a<-1}\end{array}\right.$,
∵a>$\frac{1}{2}$,∴2a>1,则ln2a>0,则不等式ln2a<-1不成立,即此时不等式组无解,
综上$\frac{1}{2e}$<a<$\frac{\sqrt{2}-1}{2}$.
故答案为:$(\frac{1}{2e},\frac{{\sqrt{2}-1}}{2})$
点评 本题主要考查导数的综合应用,根据条件转化为方程f(x)=3x存在三个不相等的实根,构造函数,利用导数研究函数的极值是解决本题的关键.综合性较强,难度较大.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{\sqrt{3}}{4}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
| A. | m≥0 | B. | 0≤m≤2 | C. | -1<m<1 | D. | m<-1或m>1 |
| A. | $3-2\sqrt{3}$ | B. | $2\sqrt{3}-3$ | C. | $-\frac{7}{4}$ | D. | $\frac{3}{4}$ |
| A. | -9 | B. | -6 | C. | -3 | D. | -$\frac{1}{3}$ |
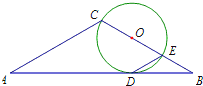 如图,在△ACB中,∠ACB=120°,AC=BC=3,点O在BC边上,且圆O与AB相切于点D,BC与圆O相交于点E,C,则∠EDB=30°,BE=1.
如图,在△ACB中,∠ACB=120°,AC=BC=3,点O在BC边上,且圆O与AB相切于点D,BC与圆O相交于点E,C,则∠EDB=30°,BE=1.