题目内容
19.设1,a+bi,b+ai是一等比数列的连续三项,则a,b的值分别为( )| A. | a=±$\frac{\sqrt{3}}{2}$,b=±$\frac{1}{2}$ | B. | a=-$\frac{1}{2}$,b=$\frac{\sqrt{3}}{2}$ | C. | a=±$\frac{\sqrt{3}}{2}$,b=$\frac{1}{2}$ | D. | a=-$\frac{1}{2}$,b=-$\frac{\sqrt{3}}{2}$ |
分析 利用等比中项及复数相等,计算即得结论.
解答 解:依题意,(a+bi)2=b+ai,
整理得:(a2-b2)+2abi=b+ai,
∴$\left\{\begin{array}{l}{{a}^{2}-{b}^{2}=b}\\{2ab=a}\end{array}\right.$,
解得:a=±$\frac{\sqrt{3}}{2}$、b=$\frac{1}{2}$或a=0、b=-1,
显然当a=0、b=-1时不满足题意,
∴a=±$\frac{\sqrt{3}}{2}$、b=$\frac{1}{2}$,
故选:C.
点评 本题考查等比数列的性质,注意解题方法的积累,属于中档题.

练习册系列答案
相关题目
11.cos$\frac{π}{12}$+$\sqrt{3}$sin$\frac{π}{12}$的值为( )
| A. | -$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | $\frac{1}{2}$ | D. | $\sqrt{3}$ |
8.函数f(x)=ex-ax-1在R上单调递增,则实数a的取值范围为( )
| A. | R | B. | [0,+∞) | C. | (-∞,0] | D. | [-1,1] |
9.函数f(x)=-cosx•lg|x|的部分图象是( )
| A. | 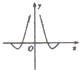 | B. | 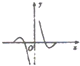 | C. | 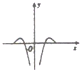 | D. | 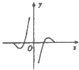 |
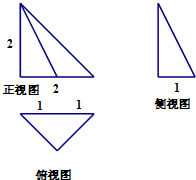 某三棱锥的三视图如右图所示,则该三棱锥的最长棱的棱长为$2\sqrt{2}$.
某三棱锥的三视图如右图所示,则该三棱锥的最长棱的棱长为$2\sqrt{2}$.