题目内容
(本小题满分12分)已知SA⊥平面ABC, SA=AB,AB⊥BC,SB=BC,E是SC的中点,
SA=AB,AB⊥BC,SB=BC,E是SC的中点,
DE⊥SC交AC于D.
求二面角E—BD—C的大小.
 SA=AB,AB⊥BC,SB=BC,E是SC的中点,
SA=AB,AB⊥BC,SB=BC,E是SC的中点,DE⊥SC交AC于D.
|
解:由(1)SC⊥BD∵SA⊥面ABC∴SA⊥BD∴BD⊥面SAC∴∠EDC为二面角E-BD-C的平面角 设SA=AB=a,则SB=BC= .
.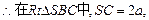

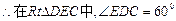 .
.
 .
.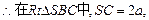

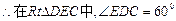 .
.略

练习册系列答案
相关题目
题目内容
 SA=AB,AB⊥BC,SB=BC,E是SC的中点,
SA=AB,AB⊥BC,SB=BC,E是SC的中点,
|
 .
.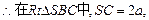

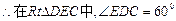 .
.