题目内容
(12分)如图,已知四棱柱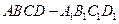 的棱长都为
的棱长都为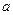 ,底面
,底面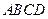 是菱形,且
是菱形,且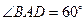 ,侧棱
,侧棱 ,
,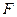 为棱
为棱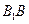 的中点,
的中点,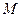 为线段
为线段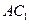 的中点.
的中点.
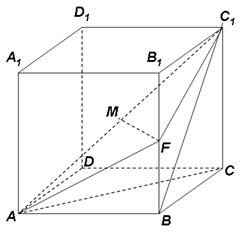
(Ⅰ)求证:平面 ;
;
(Ⅱ)求三棱锥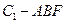 的体积.
的体积.
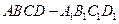 的棱长都为
的棱长都为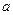 ,底面
,底面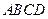 是菱形,且
是菱形,且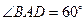 ,侧棱
,侧棱 ,
,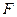 为棱
为棱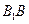 的中点,
的中点,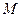 为线段
为线段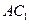 的中点.
的中点.
(Ⅰ)求证:平面
 ;
;(Ⅱ)求三棱锥
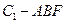 的体积.
的体积.(1)
、连接
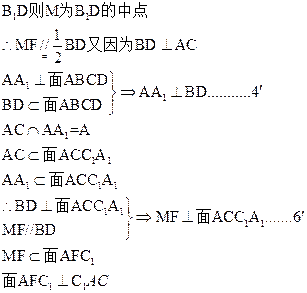
(2)
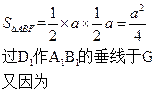

∠BAD=
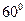
∠
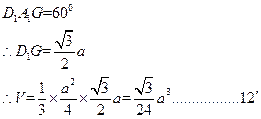
略

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
题目内容
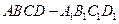 的棱长都为
的棱长都为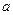 ,底面
,底面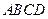 是菱形,且
是菱形,且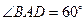 ,侧棱
,侧棱 ,
,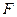 为棱
为棱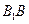 的中点,
的中点,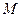 为线段
为线段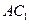 的中点.
的中点.
 ;
;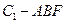 的体积.
的体积.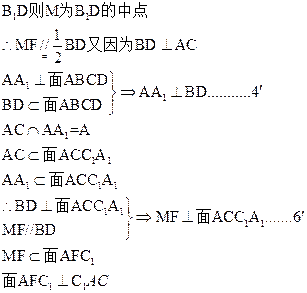
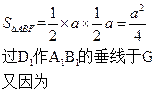

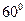
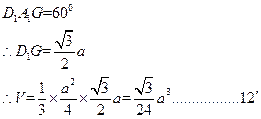

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案