题目内容
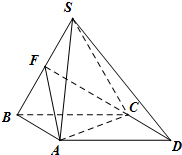
四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠DAB=135°,BC=2
,SB=SC=AB=2,F为线段SB的中点.
(Ⅰ)求证:SD∥平面CFA;
(Ⅱ)求面SCD与面SAB所成二面角大小.
| 2 |
(Ⅰ)求证:SD∥平面CFA;
(Ⅱ)求面SCD与面SAB所成二面角大小.

(Ⅰ)连结BD交AC于点E,连结EF,
∵底面ABCD为平行四边形,∴E为BD的中点.(2分)
在△BSD中,∵F为SB的中点,∴EF∥SD,(3分)
又∵EF?面CFA,SD?面CFA,∴SD∥平面CFA.(5分)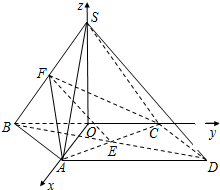
(Ⅱ)以BC的中点O为坐标原点,
分别以OA,OC,OS为x,y,z轴,建立如图所示的坐标系.
∵∠DAB=135°,BC=2
,SB=SC=AB=2,F为线段SB的中点,
∴A(
,0,0),B(0,-
,0),S(0,0,
),C(0,
,0),
∴
=(
,0,-
),
=(0,-
,-
),
=(0,-
,
),
=
=(
,
,0),(7分)
设平面SAB的一个法向量为
=(x,y,z)
由
,得
,
令z=1得:x=1,y=-1,∴
=(1,-1,1).(9分)
同理设平面SCD的一个法向量为
=(a,b,c)
由
,得
,
令b=1得:a=-1,c=1,
∴
=(-1,1,1).(10分)
设面SCD与面SAB所成二面角为θ
∴cosθ=|cos<
,
>|=|
|=
,
∴θ=arccos
.(12分)
∵底面ABCD为平行四边形,∴E为BD的中点.(2分)
在△BSD中,∵F为SB的中点,∴EF∥SD,(3分)
又∵EF?面CFA,SD?面CFA,∴SD∥平面CFA.(5分)

(Ⅱ)以BC的中点O为坐标原点,
分别以OA,OC,OS为x,y,z轴,建立如图所示的坐标系.
∵∠DAB=135°,BC=2
| 2 |
∴A(
| 2 |
| 2 |
| 2 |
| 2 |
∴
| SA |
| 2 |
| 2 |
| SB |
| 2 |
| 2 |
| CS |
| 2 |
| 2 |
| CD |
| BA |
| 2 |
| 2 |
设平面SAB的一个法向量为
| n1 |
由
|
|
令z=1得:x=1,y=-1,∴
| n1 |
同理设平面SCD的一个法向量为
| n2 |
由
|
|
令b=1得:a=-1,c=1,
∴
| n2 |
设面SCD与面SAB所成二面角为θ
∴cosθ=|cos<
| n1 |
| n2 |
| ||||
|
|
| 1 |
| 3 |
∴θ=arccos
| 1 |
| 3 |

练习册系列答案
相关题目


 是已知的平面向量,向量
是已知的平面向量,向量 ,
,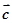 在同一平面内且两两不共线,有如下四个命题:
在同一平面内且两两不共线,有如下四个命题: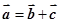 ;
; 和
和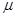 ,使
,使 ;
; =2,存在单位向量
=2,存在单位向量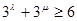
 的右顶点、左焦点分别为A、F,点B(0,-b),
的右顶点、左焦点分别为A、F,点B(0,-b), ,则双曲线的离心率值为( )
,则双曲线的离心率值为( )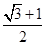 (B)
(B) (C)
(C) (D)
(D)
 的方程有
的方程有 ,则
,则


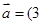 ,
, ,
, ,
, ,且
,且 ∥
∥ ,则
,则 = .
= .