题目内容
6.已知函数f(x)的导函数为f′(x),满足xf′(x)+2f(x)=$\frac{lnx}{x}$,且f(e)=$\frac{1}{2e}$,则f(x)在(0,+∞)上的单调性为( )| A. | 先增后减 | B. | 单调递增 | C. | 单调递减 | D. | 先减后增 |
分析 根据$xf′(x)+2f(x)=\frac{lnx}{x}$得到x2f′(x)+2xf(x)=lnx,从而得到[x2f(x)]′=lnx,从而x2f(x)=xlnx-x+c,由条件f(e)=$\frac{1}{2e}$即可求出c,从而求出f(x),然后求导,根据导数符号即可判断f(x)的单调性.
解答 解:∵$xf′(x)+2f(x)=\frac{lnx}{x}$;
∴x2f′(x)+2xf(x)=lnx;
∴[x2f(x)]′=lnx;
∴x2f(x)=xlnx-x+c;
∵$f(e)=\frac{1}{2e}$;
∴${e}^{2}•\frac{1}{2e}=e-e+c$;
∴$c=\frac{e}{2}$;
∴${x}^{2}f(x)=xlnx-x+\frac{e}{2}$;
∴$f(x)=\frac{lnx-1}{x}+\frac{e}{2{x}^{2}}$;
∴$f′(x)=\frac{2x-xlnx-e}{{x}^{3}}$;
令g(x)=2x-xlnx-e,g′(x)=1-lnx;
∴x∈(0,e)时,g′(x)>0,x∈(e,+∞)时,g′(x)<0;
∴g(e)=0是g(x)的最大值;
∴f′(x)≤0恒成立;
∴f(x)是减函数.
故选:C.
点评 考查积的导数和商的导数的计算公式,已知一个函数的导函数,可以写出这个函数的解析式,根据函数导数求函数最值的方法与过程,根据函数导数符号判断函数单调性的方法,注意正确求导.

练习册系列答案
相关题目
16.下列函数不等式中正确的是( )
| A. | tan$\frac{4}{7}$π>tan$\frac{3}{7}$π | B. | tan$\frac{2}{5}$π<tan$\frac{3}{5}$π | ||
| C. | tan(-$\frac{13}{7}$π)>tan(-$\frac{15}{8}$π) | D. | tan(-$\frac{13}{14}$π)<tan(-$\frac{12}{5}$π) |
17.为了解某班学生喜爱打篮球是否与性别有关,对本班50人进行了问卷调查得到了如下的列联表:
己知在全部50人中随机抽取1人抽到不喜爱打篮球的学生的概率为$\frac{2}{5}$.
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由:
(3)己知喜爱打篮球的10位女生中,A1,A2,A3还喜欢打乒乓球,B1,B2,B3还喜欢打羽毛球,C1,C2还喜欢踢足球,现在从喜欢打乒乓球、喜欢打羽毛球、喜欢踢足球的8位女生中各选出1名进行其他方面的调查,求B1和C1不全被选中的概率.(下面的临界值表供参考)
(参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$,其中n=a+b+c+d)
| 喜爱打篮球 | 不喜爱打篮球 | 合计 | |
| 男生 | 5 | ||
| 女生 | 10 | ||
| 合计 | 50 |
(1)请将上面的列联表补充完整;
(2)是否有99.5%的把握认为喜爱打篮球与性别有关?说明你的理由:
(3)己知喜爱打篮球的10位女生中,A1,A2,A3还喜欢打乒乓球,B1,B2,B3还喜欢打羽毛球,C1,C2还喜欢踢足球,现在从喜欢打乒乓球、喜欢打羽毛球、喜欢踢足球的8位女生中各选出1名进行其他方面的调查,求B1和C1不全被选中的概率.(下面的临界值表供参考)
| p(K2≥k) | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
18.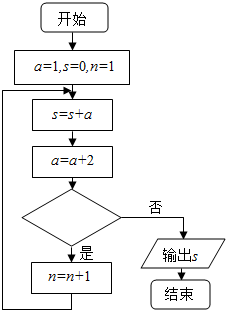 阅读如图所示的程序框图,运行相应的程序,若输出的结果s=9,则图中菱形内应该填写的内容是( )
阅读如图所示的程序框图,运行相应的程序,若输出的结果s=9,则图中菱形内应该填写的内容是( )
 阅读如图所示的程序框图,运行相应的程序,若输出的结果s=9,则图中菱形内应该填写的内容是( )
阅读如图所示的程序框图,运行相应的程序,若输出的结果s=9,则图中菱形内应该填写的内容是( )| A. | n<2 | B. | n<3 | C. | n<4 | D. | a<3 |