��Ŀ����
7����ֱ֪��L��$\left\{\begin{array}{l}{x=-1+tcos��}\\{y=tsin��}\end{array}\right.$������C��$\left\{\begin{array}{l}{x=\sqrt{2}cos��}\\{y=sin��}\end{array}\right.$�ཻ��A��B���㣬��F������Ϊ��1��0������1�����ABF���ܳ���
��2������E��-1��0��ǡΪ�߶�AB�����ȷֵ㣬��������ABF�������
���� ��1������ͬ�ǵ�ƽ����ϵ�ʹ��뷨������������Ϊ��ͨ���̣�������Բ�Ķ��壬���ɵõ�����������ABF���ܳ���
��2������ֱ�߷��̺���Բ���̣���ȥx������Τ�ﶨ�������ȷֵ㣬���|y1-y2|���������������ε������ʽ�����㼴�ɵõ���
��� �⣺��1������C��$\left\{\begin{array}{l}{x=\sqrt{2}cos��}\\{y=sin��}\end{array}\right.$��Ϊ��ͨ����Ϊ$\frac{{x}^{2}}{2}$+y2=1��
ֱ��L��$\left\{\begin{array}{l}{x=-1+tcos��}\\{y=tsin��}\end{array}\right.$��Ϊ��ͨ����Ϊy=tan��•��x+1����
ֱ�ߺ����Բ����F'��-1��0����
����Բ�Ķ���ɵã���ABF���ܳ�Ϊ|AF'|+|AF|+|BF'|+|BF|=4a=4$\sqrt{2}$��
��2����A��x1��y1����B��x2��y2����
��ֱ�߷��̴�����Բ���̣���ȥx���ɵã�
��2+cot2����y2-2cot��•y-1=0��
��y1+y2=$\frac{2cot��}{2+co{t}^{2}��}$��y1y2=-$\frac{1}{2+co{t}^{2}��}$����
��E��-1��0��ǡΪ�߶�AB�����ȷֵ㣬����2y1=-y2����
���cot��=��$\frac{\sqrt{14}}{7}$��
���ABF�����ΪS=$\frac{1}{2}$|FF'|•|y1-y2|=|y1-y2|=$\sqrt{��{y}_{1}+{y}_{2}��^{2}-4{y}_{1}{y}_{2}}$
=$\sqrt{��\frac{��\frac{2\sqrt{14}}{7}}{2+\frac{2}{7}}��^{2}+\frac{4}{2+\frac{2}{7}}}$=$\frac{3\sqrt{14}}{8}$��
���� ������Ҫ����������̺���ͨ���̵Ļ�����ͬʱ������Բ�Ķ����ֱ�ߺ���Բ��������������Τ�ﶨ�����ҳ���ʽ���������������������е��⣮

| ϲ�������� | ��ϲ�������� | �ϼ� | |
| ���� | 5 | ||
| �� | 10 | ||
| �ϼ� | 50 |
��1���뽫���������������������
��2���Ƿ���99.5%�İ�����Ϊϲ�����������Ա��йأ�˵��������ɣ�
��3����֪ϲ���������10λŮ���У�A1��A2��A3��ϲ����ƹ����B1��B2��B3��ϲ������ë��C1��C2��ϲ�����������ڴ�ϲ����ƹ����ϲ������ë��ϲ���������8λŮ���и�ѡ��1��������������ĵ��飬��B1��C1��ȫ��ѡ�еĸ��ʣ���������ٽ�ֵ�����ο���
| p��K2��k�� | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
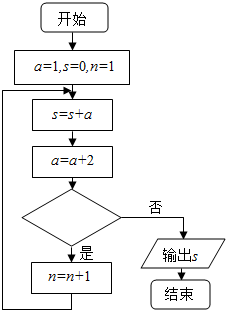 �Ķ���ͼ��ʾ�ij����ͼ��������Ӧ�ij���������Ľ��s=9����ͼ��������Ӧ����д�������ǣ�������
�Ķ���ͼ��ʾ�ij����ͼ��������Ӧ�ij���������Ľ��s=9����ͼ��������Ӧ����д�������ǣ�������| A�� | n��2 | B�� | n��3 | C�� | n��4 | D�� | a��3 |